第四章 命题与证明测试
姓名：
一．选择题：（每小题4分,共16分.）
1．下列描述不属于定义的是： （ ）
A．两组对边分别平行的四边形是平行四边形。
B．正三角形是特殊的三角形。
C．在同一平面内三条线段首尾相连得到的图形是三角形。
D．含有未知数的等式叫做方程。
2．下列语句不是命题的为： （ ）
A．同角的余角相等。 B. 作直线AB的垂线。
C．若a-c=b-c，则a=b D. 两直线相交，只有一个交点。
3．下列命题中的真命题是： （ ）
A．锐角大于它的余角。 B. 锐角大于它的补角。
C．钝角大于他的补角。 D. 锐角与钝角之和等于平角。
4．满足下列条件的△ABC中，不是直角三角形的是： （ ）
A．∠B+∠A=∠C。 B. ∠A：∠B：∠C=2：3：5.
C. ∠A=2∠B=3∠C. D. 一个外角等于和它相邻的一个内角.
二．把下列命题改写成“如果······，那么······”的形式。
（每小题4分,共16分）
⑴对顶角相等；
⑵在同一个三角形中,等角对等边.
⑶等角的余角相等；
(4)正方形是轴对称图形；
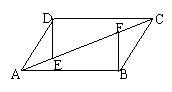
三. 如图：已知AD∥BC，AD=BC，AE=CF.求证：DE∥BF（10分）
 |
四.
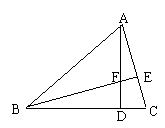
如图：已知AD为ΔABC的高，E为AC上一点，BE交AD于F，且有BF=AC，FD=CD，
求证：BE⊥AC（10分）
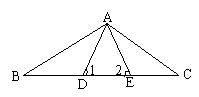五．如图，点B、D、E、C在同一条直线上，且∠1=∠2，BD=EC，求证：ΔABE≌ΔACD（10分）
六.如图在ΔABC中AB=AC,∠BAC=900,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F
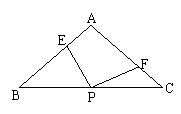⑴求证：AE=CF
⑵是否还有其他结论（12分）
七．如图：已知点C在AB上，ΔACD与ΔCBE是等边三角形，连结AE、BD分别交CD、CE于点M、N。
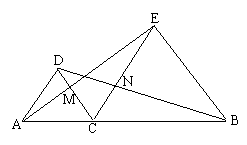求证：（1）AE=BD （2）CM=CN（12分）
八.如图:已知等腰直角三角形ABC中,∠ACB=90°,直线L经过点C,AD⊥L,
BE⊥L,垂足分别为D、E
(1)证明：ΔACD≌ΔCBE
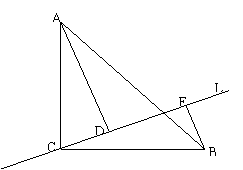
(2)如图,当直线L经过ΔABC内部时,其他条件不变,这个结论还是真命题吗?如果是真命题,请给出证明;如果是假命题,请说明理由. （14分）