八年级第三次学业评估
一、选一选（每小题3分，共24分）
1、下列运算正确的是（ ）
A．
B．
C．-3
+=-2
D．
2、如果
是二次根式，那么
应适合的条件是（ ）
A、≥3 B、≤3 C、＞3 D、＜3
3、下面是某同学在一次数学测验中解答的填空题，其中答对的是（ ）
A、若
；
B、
；
C、
；
D、
的值为零，则
。
4、命题：①对顶角相等；②垂直于同一条直线的两直线平行；③相等的角是对顶角；④同位角相等.其中假命题有（ ）
A、1个 B、2个 C、3个 D、4个
5、下列图形既是轴对称图形，又是中心对称图形的是（ ）
A、等边三角形 B、矩形 C、平形四边形 D、等腰梯形
7、某人到瓷砖商店去购买一种多边形形状的瓷砖，用来铺设无缝地板．他购买的瓷砖形状不可以是（ ）．
（A）正三角形 （B）正四边形 （C）正八边形 （D）正六边形
6、平行四边形一边长为12cm，那么它的两条对角线的长度可能是（ ）．
（A）8cm和14cm （B）10cm和14cm （C）18cm和20cm （D）10cm和34cm
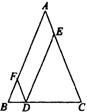
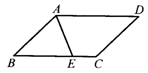
7、如图,在
中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,
那么四边形AFDE的周长是 ( )
A.5 B.10 C.15 D.20
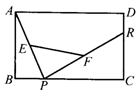
8、如图，已知矩形ABCD，R，P分别是DC，BC上的点，E，F分别是AP，RP的中点．当点P在BC上从点B向点C移动而点R不动时，那么下列结论成立的是（ ）．
（A）线段EF的长逐渐增大 （B）线段EF的长逐渐减少
（C）线段EF的长不变 （D）线段EF的长不能确定
（8） （7）
二、填一填（每小题3分，共24分）
9、化简：
= ，
=
，
=
。
10、当
时，关于的方程
为一元二次方程。
11.已知方程3ax2-bx-1=0和ax2+2bx-5=0,有共同的根-1, 则a= , b= .
12、平行四边形的一组对角的和为280°，则其相邻的两个内角分别为_______．
13．如图，在平行四边形ABCD中，∠A的平分线交BC于点E．若AB=10cm，AD=14cm，则BE=______，EC=________．
14、如图3，A，B两点分别位于一个池塘的两端，小明想用绳子测量A，B间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接达到A，B的点C，找到AC，BC的中点D，E，并且测出DE的长为15m，则A，B两点间的距离为_____m．
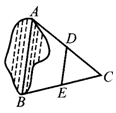
（14） （13）
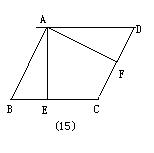
15、如图12-52,在▱ABCD中,AE⊥BC于E,AF⊥CD于F,BE=3厘米,AB=6厘米,DF=5厘米,则▱ABCD的周长为________厘米.
16、已知，在三角形ABC中，AB=5，AC=4，则BC边上的中线AD的取值范围为_______________
三、做一做（17题12分，18、19、20、21、22题6分， 23题10分）
17、解方程
（1）
（2）
18、请说出“等腰三角形两腰上的高相等”的逆命题．这个逆命题是真命题吗？请证明你的判断．
19、如图，在平行四边形ABCD中，DB=CD，∠C=70°，AE⊥BD于点E．试求∠DAE.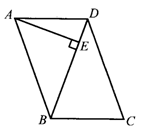 
20、已知：如图，在四边形ABCD中，AB=DC，AD=BC，点E在BC上，点F在AD上，AF=CE，EF与对角线BD相交于点O，求证：O是BD的中点
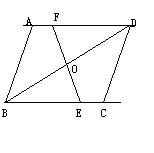
21、已知：如图，在平行四边形ABCD中，E，F分别是AD，BC的中点．求证：MN∥BC，且MN=
BC
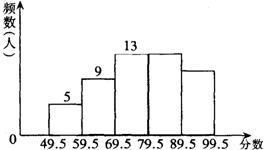
22．某中学八年级共有400名学生，学校为了增强学生的国防意识，在本年级进行了一次国防知识测验．为了了解这次测验的成绩状况，从中抽取了50名学生的成绩，将所得数据整理后，画出频数分布直方图如图所示．
(1)图中第四个小组和第五个小组的频率各是多少?第五个小组的频数是多少?
(2)这次测验中，八年级全体学生优秀成绩（80或80以上）的人数是多少?
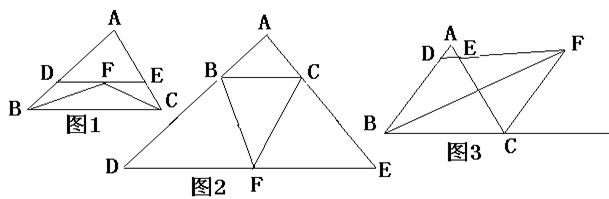
26、（1）如图1在△ABC中，∠ABC的平分线BF与∠ACB的平分线CF相交于F，过点F作DE∥BC，交直线AB于点D，交直线AC于点E，求证：BD+CE=DE
（2）如图2，△ABC的外角平分线BF、CF相交于F，过点F作DE∥BC，交直线AB于点D，交直线AC于点E，那么BD，CE，DE之间存在什么关系？
（3） 图3，∠ABC的平分线BF与∠ACB的外角平分线CF相交于F，过点F作DE∥BC，交直线AB于点D，交直线AC于点E，那么BD，CE，DE之间存在什么关系？根据（1）、（2）写出你的猜想，并证明你的结论。
