北师大版数学八年级（下）第四章《相似图形》训练
一、选择题
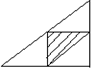1.厨房角柜的台面是三角形（如图所示），如果把各边中点连线所围成的三角形铺成黑色大理石（图中阴影部分），其余部分铺成白色大理石，那么黑色大理石的面积与白色大理石面积的比是（ ）
（A） 
（B） 
（C） 
（D） 
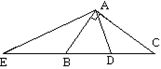
2.如图，在△ABC中，∠BAC=90,D是BC中点，AE⊥AD交CB的延长线于E,则下列结论正确的是（ ）
（A）△AED∽△ACB （B） △AEB∽△ACD
（C） △BAE∽ △ACE （D） △AEC∽△DAC
3.在梯形ABCD中，AD∥BC.AC,BD相交于O ,如果AD：BC=1：3, 那么下列结论正确的是（ ）
（A） S△COD =9 S△AOD （B） S△ABC =9 S△ACD （C） S△BOC =9 S△AOD （D） S△DBC =9 S△AOD
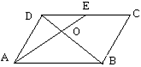
4.如图，在平行四边形ABCD中，E为CD中点， AE交BD于O，S△DOE =12㎝2，则S△AOB等于（ ）
（A）24㎝2 （B） 36㎝2 （C） 48㎝2 （D） 60㎝2
5. 如果线段AB=10，点C是AB上靠近点B的黄金分割点，则AC的值为（ ）
（A） 0.168 （B）6.18 （C） 3.82 （D） 6.18或3.82
6.如果mn=ab,则下列比列式中错误的是（ ）
（A） 
（B） 
（C） 
（D）
7.如图，在大小为4×4的正方形网格中，是相似三角形的是（ ）
 |
① ② ③ ④
（A）①和② （B） ②和③ （C） ①和③ （D） ②和④
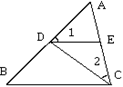
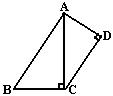8.如图，若∠1=∠2=∠B，则图中相似三角形有（ ）
（A） 1对 （B）2对 （C）3对 （D） 4对
9.如果
，且a+b+c
.则k的值为（ ）
（A） （B） 
（C） 或-1 （D） -1
10.如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使⊿ABC∽⊿CAD,只要CD等于( )
（A）
（B）
（C）
（D）
二、填空题：11，一竹竿高1.5米，影长1米，同一时刻，某塔影长20米，则塔高为 米。
12，已知△ABC∽△DEF,且△ABC的三边长分别为
△DEF的两边长分别为1,
,则第三边长为
13.在△ABC中，DE为平行BC的截线，若
，则
= .
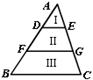
14.如图，AD=DF=FB，DE∥FG∥BC，则SⅠ∶SⅡ∶SⅢ= .
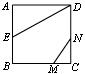
15.如图，正方形ABCD的边长为2，AE=EB，MN=1，线段MN的两端在CB、CD上滑动，当
CM= 时，ΔAED与N，M，C为顶点的三角形相似.
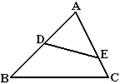
16.如图,⊿ABC中,D,E分别是AB,AC上的点(DE
BC),当 或 或 时,⊿ADE与
⊿ABC相似.
班 姓名 座号
 | |||
 | |||
（第16题图） （第14题图） （第15题图）
三、解答题
17. 一条河的两岸有一段是平行的，在该河岸的这一段每隔5米有一颗树，河对岸每隔50米有一根电线杆。在这岸离开岸边25米处看对岸，看到对岸相邻d两根电线杆恰好被这岸的两颗树遮住，且这两颗树之间还有3克棵树，求河的宽度。
18.如图,⊿ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F.
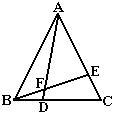(1)试说明⊿ABD≌⊿BCE.
(2)⊿AEF与⊿ABE相似吗?说说你的理由.
(3)BD2=AD·DF吗?请说明理由.
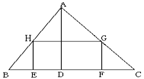
19.在△ABC中有一内接矩形，矩形的一边EF在BC上，两顶点H、G分别在AB、AC上，若HE:HG＝3:4，BC=20cm，三角形的高AD=15cm，求矩形的两邻边长。
四、探索题
20.已知：如图，ΔABC中，∠B=∠C=30°.请你设计三种不同的分法，将ΔABC分割成四个三角形，使得其中两个是全等三角形，而另外两个是相似三角形但不全等的直角三角形.请画出分割线段，标出能够说明分法的所得三角形的顶点和内角度数或记号，并在各种分法的空格线上填空.(画图工具不限，不要求写出画法，不要求说明理由).
 | | |
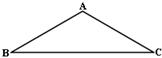分法一 分法二 分法三
分法一：分割后所得的四个三角形中，Δ ≌Δ ，RtΔ ∽RtΔ .
分法二：分割后所得的四个三角形中，Δ ≌Δ ，RtΔ ∽RtΔ .
分法三：分割后所得的四个三角形中，Δ ≌Δ ，RtΔ ∽RtΔ .