八年级（下）数学月测验分析卷
班级________, 学号______ ，姓名______
一、填空题(每题3分，共30分)
1． 若一个实数的平方根等于它的立方根，则这个数是_________．
2．
的相反数是_______．
3．
数轴上表示
的点与原点的距离是________．
4．
计算：
．
5．
在
，
，０，
，
，
，0.中，无理数是______________．
6．
已知P点在第二象限，且到
轴距离是2，到
轴距离是3，则P点的坐标是___________________
7． 已知一次函数y=－mx＋(m－2)，若它的图象经过原点，则m=_________；若图象经过一、三、四象限，则m的取值范围是__________
8．
的平方根是_______．
9．
当
时，
有意义．
10．若
，
，则
的所有可能的值为________________。
二、选择题(每题3分，共24分)
11、若点P(2m-1,m+3)在第二象限，则m的取值范围是 （ ）
A、
B、
C、
D、 
12、已知直线
不经过第四象限，则
的取值是_____________________
13、下列说法不正确的是 ( )
A．
是36的一个平方根； B．6是36的一个平方根；
C．36的平方根是6； D．36的平方根是
14、若点A关于x轴的对称点的坐标为（－1，2），则A点的坐标是（ ）
A．（－1，－2） B．（1，2）
C．（1，－2） D．（－1，2）
15、下列说法中，不正确的是 ( )
A．非负数的非负平方根是它的算术平方根
B．非负数的立方根就是它的三次算术根
C．一个负数的立方根只有一个，且仍是负数；
D．一个数的立方根总比平方根小
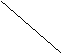
16、一次函数y=kx－b的图象（其中k<0，b>0）大致是 （ ）
y
y
y
y
 |  | ||||
 | |||||
x
x
x
x
A B C D
17、下列函数中自变量x的取值范围是x
2的是（ ）
A．y=
B．y=
C．y=
D．y=
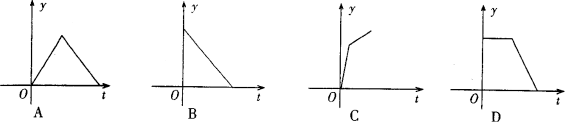
18、某产品的生产流水线每小时可生产100件产品，生产前没有产品积压，生产3h后安排工人装箱，若每小时装产品150件，未装箱的产品数量y是时间t的函数，这个函数的大致图象只能是下图中的（ ）
八年级（下）数学月测验分析卷
班级________, 学号______ ，姓名______，成绩______
一、填空题(每题3分，共30分)
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 答案 |
| 题号 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、选择题(每题3分，共24分)
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 答案 |
二、解答题（共66分）
19、求下列各式中的x．(每题3分，共6分)
⑴ 
⑵
20、计算：(每题3分，共12分)
⑴ 
⑵
⑶ 
⑷
21、已知一次函数y= -2x + 1, 利用图象, 求当x取什么值时, -3＜y＜3 .（6分）
 |
22、已知一次函数的图象经过点
。
（1）求此一次函数的解析式；(3分)
（2）求此函数与轴、轴的交点坐标；（4分）
（3）作出此一次函数的图象；（3分）
（4）求出此函数图象与坐标轴围成的三角形的面积．（4分）
 |
23、已知y＝++3，求+ (6分)
24、已知
，求
的值．(6分)
25、双曲线
和直线
相交于
、
，双曲线和直线
相交于两点、
，已知的纵坐标是4. ⑴求点、、的坐标。（6分）⑵求二直线与y轴围成的三角形的面积。(4分)
26、市欲将一批容易变质的水果运往市销售，共有飞机、火车、汽车三种运输方式，现只可选择其中的一种，这三种运输方式的主要参考数据如下表所示：
| 运输工具 | 途中速度（km/h） | 途中费用（元/千米） | 装卸费用（元） | 装卸时间（t） |
| 飞机 | 200 | 16 | 1000 | 2 |
| 火车 | 100 | 4 | 2000 | 4 |
| 汽车 | 50 | 8 | 1000 | 2 |
若这批水果在运输（包括装卸）过程中的损耗为每小时200元，记A、B两市间的距离为km。
⑴如果用
、
、
分别表示使用飞机、火车、汽车运输时的总支出费用（包括损耗），求出、、与的函数关系式；（6分）
⑵应采用哪种运输方式才能使运输时的总支出费用最小？（4分）