泽国二中八年级数学竞赛试卷
一、选择题（每小题5分，共40分）
1、已知反比例函数y=
的图象上两点A（x1，y1），B（x2，y2），当x1＜0＜x2时，有y1＜y2，则m的取值范围是
（
）
A. m＜1 B、m＞1 C、m＞2 D、m＜2
2．.如图a，ABCD是一矩形纸片，AB=6cm，AD=8cm,E是AD上一点，且AE=6cm，操作：⑴将AB向AE折过去，使AB与AE重合，得折痕AF，如图b；⑵将△AFB以BF为折痕向右折过去，得图c，则△GFC的面积为( )
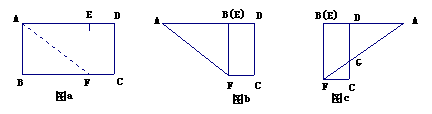
A.2 B. 3 C. 4 D.
3．若方程
有正数根,则k的取值范围是( )
（A）
（B）
（C） 
（D）
4.把5个整数从小到大排列，则中位数是4，如果这5个数的唯一众数是6，则这5个整数可能的最大和是（ ）
A、21 B、22 C、23 D、24
5、古人用天干和地支记次序，其中天干有10个：甲乙丙丁戊己庚辛壬癸。地支也有12个：子丑寅卯辰巳午未申酉戌亥，将天干的10个汉字和地支的12个汉字分别循环排列成如下两行：
甲乙丙丁戊己庚辛壬癸甲乙丙丁戊己庚辛壬癸……
子丑寅卯辰巳午未申酉戌亥子丑寅卯辰巳午未申酉戌亥……
从左向右数，第1列是甲子，第2列是乙丑，第3列是丙寅……，则当第2次甲和子在同一列时，该列的序号是（ ）
A. 31 B. 61 C. 91 D. 121
6.如图-5所示，两个边长都为2的正方形ABCD和OPQR，如果
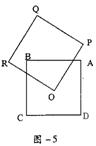O点正好是正方形ABCD的中心，而正方形OPQR可以绕O点旋转，
那么它们重叠部分的面积为（ ）
A、4 B、2
C、1 D、
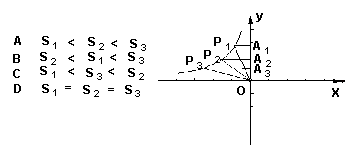
7.如图所示，
是双曲线上的三点，过这三点分别作
轴的垂线，得到三个三角形，分别是
设它们的面积分别是
则 （ ）
8.将一长方形切去一角后得一边长分别为13、19、20、25和31的五边形（顺序不一定按此）,则此五边形的面积为（ ）
A、680 B、720 C、745 D、760
二、填空题（每小题5分，共30分）
9、映在镜子里的这个号码（如图）的实际号码是_________.
10.将两个全等的有一个角为
的直角三角形如图1拼放，使其两条较长直角边在同一直线上，那么图中的等腰三角形共有 个。
 |  | ||||
| |||||
11、已知AD是
的中线，
，把
沿AD所在直线对折，点C落在点E的位置(如图4)，则
等于 度。
12、直角三角形的两条直角边分别长5和12，三角形内一点到三边的距离都为d, 则d= .
13、甲、乙、丙、丁四人参加一次数学竞赛.赛后,他们四个人预测名次的谈话如下:
甲:“丙第一名，我第三名.”
乙：“我第一名，丁第四名.”
丙：“丁第二名，我第三名.”
丁没说话.
最后公布结果时,发现他们预测都只对了一半.请你说出这次竞赛的甲、乙、丙、丁四人的名次.
甲是第 名,
14．汽车以每小时72千米的速度笔直地开向寂静的山谷，驾驶员按一声喇叭，4秒后听到回响，已知声音的速度是每秒340米，听到回响时汽车离山谷听距离是_________米
三、解答题：（共50分）
15、正方形通过剪切可以拼成三角形，方法如下
 |
仿照上例，用图示的方法，解答下列问题：（操作设计）
（1）、如图，对直角三角形，设计一种方案，将它分成若干块，再拼成一个与原三角形等面积的矩形
（2）、如图，对任意三角形，设计一种方案，将它分成若干块，再拼成一个与原三角形面积等的矩形
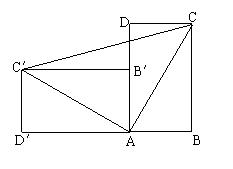16、一个直立的火柴盒在桌面上到下，启迪人们发现了勾股定理的一种新的证明方法，如图火柴盒的一个侧面ABCD倒下到AB′C′D′的位置，连接CC′，设AB=a，BC=b,AC=c，请利用四边形BCC′D′的面积证明勾股定理:a2＋b2=c2.
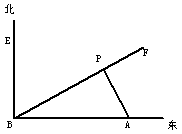
17、如图，A城气象台测得台风中心在A城正西方向320km的B处，以每小时40km的速度向北偏东60°的BF方向移动，距离台风中心200km的范围内是受台风影响的区域。
⑴A城是否受到这次台风的影响？为什么？
⑵若A城受到这次台风影响，那么A城遭受这次台风影响有多长时间？
18、如图，四边形ABCD是直角梯形，∠B=900，AB=8cm，AD=24cm，BC=26cm，点P从A点出发，以1cm/s的速度向D运动,点Q从C同时出发,以3cm/s的速度向B运动,其中一个动点到达端点时,另一个动点也随之停止运动. （8分）
①从运动开始,经过多少时间,四边形PQCD成为平行四边形/成为等腰梯形?
②设梯形ABQP的面积为y,运动的时间x,写出y与x之间的函数关系式,并写出自变量的取值范围;
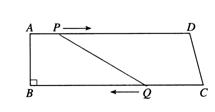③求当x等于多少时,ABQP的面积是ABCD的一半?
19、如图，四边形ABCD中，AC=6，BD=8且AC⊥BD顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1；再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2……如此进行下去得到四边形AnBnCnDn .
（1）证明：四边形A1B1C1D1是矩形；
（2）写出四边形A1B1C1D1和四边形A2B2C2D2的面积；
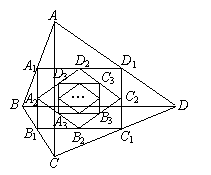（3）写出四边形AnBnCnDn的面积；
（4）求四边形A5B5C5D5的周长.
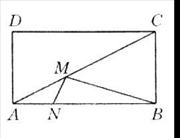（本题15分）矩形ABCD中，AB=20，BC=10，若在AC、AB上各取一点M、N（如图），使BM+MN的值最小，求这个最小值。（15分）
、如图6，正三角形ABC的边长为a，D是BC的中点，P是AC边上的点，连结PB和PD得到△PBD。求：
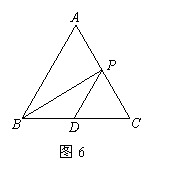⑴当点P运动到AC的中点时，△PBD的周长；
⑵△PBD的周长的最小值。
13、已知点A（1，1）在平面直角三角形系中,在坐标轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有________________个.
.在钟表面上，OA是秒针，OB是分针，现在是12：00，当三角形AOB的面积第一次达到最大时，时间经过了＿＿＿＿＿秒。
13、（本题10分）甲、乙、丙、丁四人参加一次数学竞赛.赛后,他们四个人预测名次的谈话如下:
甲:“丙第一名，我第三名.”
乙：“我第一名，丁第四名.”
丙：“丁第二名，我第三名.”
丁没说话.
最后公布结果时,发现他们预测都只对了一半.请你说出这次竞赛的甲、乙、丙、丁四人的名次.
甲是第 名,乙是第 名,丙是第 名,丁是第 名.
15. 已知，在
中，
为底边
上
任意一点，过点
分别作
的平行线交
于
，交
于
．
(1) 求四边形
的周长；
(2) 点位于的什么位置时，四边形为菱形？说明你的理由．
、如图，正方形硬纸片ABCD的边长是4，点E、F分别是AB、BC的中点，若沿左图中的虚线剪开，拼成如下右图的一座“小别墅”，则图中阴影部分的面积是（ ）
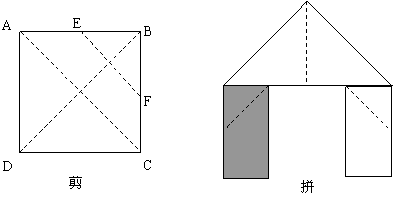A、2 B、4 C、8 D、10
|
|
