石门实验中学2005-2006学年度第二学期初二数学期末复习题(03)
几何的证明与计算专题复习
班级__________ 学号_______ 姓名______________ 得分___________
1．同一时刻，某地一根高30m的旗杆的影长为40m,一楼房的影长为50m,则这楼房的高度为多少米？
2．如果a:b:c=3:4:5,且a+b+c=36,求a,b,c的值。
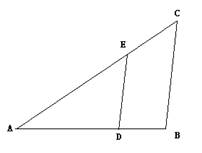
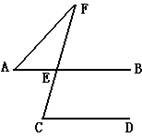
3．如图，已知△ABC∽△ADE，AD=40cm,DB=20cm,DE=50cm,∠BAC=450,
∠AED=300,（1）求∠ACB和∠B的大小。（2）求BC的长。
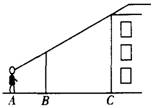4．如图，小明欲测一楼房的高度，他借助一5m长的标杆对楼房进行测量，当楼房顶部、标杆顶端与他的眼睛在一条直线上时，其它人测出AB=4m，AC=12m．已知他的眼睛离地面1.60m，请你算出楼房的高．
5．在比例尺为1∶500的地图上，一块多边形地区的面积是300cm2，求这个地区的实际面积。
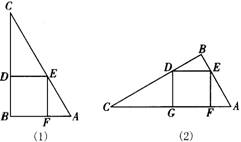
6．一块直角三角形木板的一条直角边AB长为3，BC的长为4。要把它加工成一个正方形桌面，甲、乙两人的加工方法分别为下图中的(1)、(2)所示，问哪一种方法的面积最大？并说明理由。
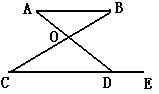7．如图，已知：∠B＝300，∠AOB＝1150，AB∥CE，试求∠ADE的度数。
8．如图，已知：AB∥CD，∠A＝500，∠C＝800，试求∠AFC的度数。
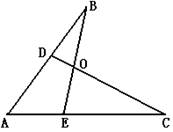9．如图，已知：D是AB上一点，E是AC上一点，BE、CD相交于O，
∠A＝580，∠BOD＝700，∠C＝300，求∠B的度数。
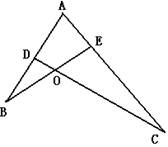10．如图，已知：AD·AB＝AE·AC，（1）△ABE与△ACD是否相似？为什么？（2）△OBD与△OCE是否相似？为什么？
11．如图，已知：矩形ABCD，沿AF折叠，点E落在CD边上，△ABF与△AEF完全重合，则△FCE与
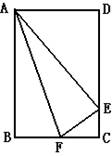△EDA是否相似？为什么？
12．如图，已知：△ABC是等边三角形，点D，E分别在BC，AC上，且BD＝CE，AD与BE相交于点F。（1）试说明△ABD≌△BCE；（2）△AEF与△BEA相似吗？说说你的理由。（3）BD2＝AD·DF吗？请说明理由。
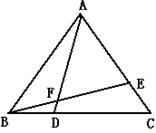
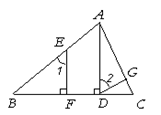
13．已知：如图，AD⊥BC，EF⊥BC，∠4=∠C．求证：∠1=∠2．
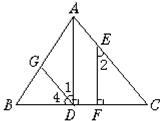
14．如图，∠1和∠D互余，CF⊥DF．求证：AB∥CD．
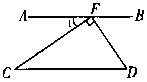
15．如图，△ABC中，D在BC的延长线上，E在CA的延长线上，F在AB上．求证：∠2>∠1．
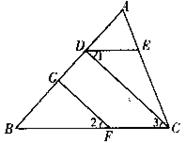
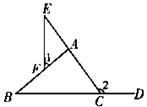
16．如图，∠ADE=∠B，∠1=∠2，GF⊥AB．求证：CD⊥AB．
17．如图，已知：AC∥DE，DC∥EF，CD平分∠BCA。求证：EF平分∠BED.
 |
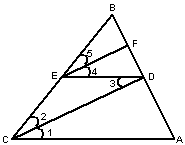
18．图中，∠A=∠F，∠C=∠D．求证:BD∥CE.
翰林汇
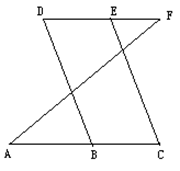
19．图中,∠ABC=∠ADC,BF和DE分别平分∠ABC和∠ADC,∠1=∠2求证:DE∥FB.
翰林汇
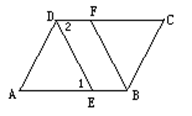
20．已知：如图，AB∥CD，AD∥BC，求证：∠B=∠D.
A D
B C
21．如下图,已知AD⊥BC,EF⊥BC,∠1=∠2. 求证：DG∥BA.
 |