解直角三角形单元测试题
一、填空题：（每空2分，共32分）
1、Rt△ABC中，∠C＝90°，AB=41，AC＝9，cosa＝____,tanA=____。
2、若锐角α、β互余且cosα＝4/5，则sinβ＝_____，cosβ＝______。
3、α为锐角，且tanα＝1，则α＝________，sinα＝________。
4、比较大小：sin68°___cos20°，ctg50°___ctg70°
5、一个斜坡的坡度i＝1：2，则坡角α的正切值为_________；若某人沿斜坡直线行进100米，则垂直高度上升了________米。
6、 6、边长为α的等边三角形，高为_________，面积为__________。
7、∠A是锐角，且sinA=
，则cos（900-A）= ；
8、在锐角△ABC中，∠A＝75°,sinC＝ ，则∠B＝
9、若cotα·tan50°=1，则锐角α=
_____度。
10、如图，在高2米，坡角为30°的楼梯表面
铺地毯，地毯的长度至少需 米。
二、选择题（每小题2分，共20分）
11、一个直角三角形,两边长分别为3和4,下列说法正确的是( )
A、第三边长为5和
; B、三角形的周长为25;
C、第三边长为5; D、三角形面积为20.
12、三角形的三边长为
,则这个三角形是 ( )
A、等边三角形; B、钝角三角形;
C、直角三角形; D、锐角三角形.
13、直角三角形中,若各边的长度都扩大5倍,那么锐角∠A的正弦( )
A、扩大5倍 B、缩小5倍 C、没有变化 D、不能确定
14、在Rt△ABC 中，∠C=90° ，则
等于
（
）
A、0 B 1 C、－1 D、不确定
15、Rt△ABC中，∠C=90°，如果sinA= ，那么cosB的值为 （ ）
|  | ||||
 | |||||
A 、 B、 C、 D、不确定
16、当A＞60°时，则tanA= （ ）
（A）
大于
（b）小于且大于0
（c）大于
（d）小于且大于0
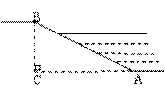17、河堤的横断面如图所示，坝高BC是5米，迎水斜坡AB的长是13米，那么斜坡AB的坡度等于：
（ ）
A、1：3 B、1：2.6
C、1:2.4 D、1:2
18、在Rt△ABC中，已知a边及∠A，则斜边应为 （ ）
 |  |
A、
B、
C、
D、
19、一个直角三角形有两条边长为3和4，则较小锐角的正切值是（ ）
A、 B、 C、 D、 或
20、已知α为锐角，tan（90°－α）=
，则α的度数为
（ ）
A、30° B、45° C、60° D、75°
三、解答题：
21、（4分）在Rt△ABC中，∠c＝90°，已知∠a＝60°，b＝
，求a、c；
22、（4分）在Rt△ABC中，∠c＝90°，c＝
，b＝3，求a、A
23、（5分）计算: sin30°·cot30°+cos60°·tan30°·cot45°
24、（5分）为了测量一棵大树的高度AB,在离树25米的C处,用高1.4米的测角仪CD测得树的顶端B的仰角α=21°,求树AB的高.(精确到0.1米，tan21°=)
B
D α
E
C
A
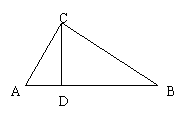
25、（7分）已知：如图，在ΔABC中，∠ACB＝90°，CD⊥AB，垂足为D，
若∠B＝30°，CD＝6，求AB的长．
 |
26、（6分）如图，某公路路基横断面为等腰梯形.按工程设计要求路面宽度为10米，坡角为60°，路基高度为5.8米，求路基下底宽（精确到0.1米）.
27、（7分）有一幢高楼19米,要在这幢楼旁东面再建一幢新楼,要求在下午15点之前这幢楼不能遮住新楼的阳光,已知15点时太阳的光线与旧楼的照射角为60°,新楼窗子底边离地面1米,那么新楼应离这幢楼多远?(精确到0.1米)
 |
28、
（10分）去年某省将地处A、B两地的两所大学合并成一所综合性大学，为了方便两地师生交往，学校准备在相距2km的A、B两地之间修一条笔直的公路，经测量在A地北偏东600方向，B地北偏西450方向的C处有一个半径为0.7km的公园，问计划修筑的这条公路会不会穿过公园？为什么？
附加题：（10分）
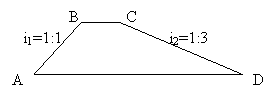
29、如图有一山坡公路横断面近似于梯形,(以梯形计算),一汽车从A驶向D,已知汽车的速度是每小时40千米,1.5分钟到达B,BC为300米,求汽车从A地到D地的路程.
| |||
 | |||