成都七中实验学校八年级下期末复习
几何练习题（总分150分）
一、填空（每小题2分，共34分） 姓名＿＿＿
1、已知
，则
；
2、若
，则
；
3、若
，则k = ；
4、宽与长的比等于黄金比的矩形也称为黄金矩形，若一黄金矩形的长为2 cm，则其宽为 cm；
5、如图，点C与点D是线段AB的两个黄金分割点，若CD = 10 cm，
则AB = cm；
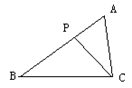
6、如图，P是△ABC中边AB上一点，连接CP，有如下条件：
①
，②
，③
，
④
，其中能判定
∽
的条件是
；
7、晚上，小明站在离路灯底部7 m远的地方，测的他的影子长为3 m，若小明身高1.8m，则路灯的高为 m；
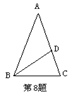
8、△ABC中，AB = AC ，BD平分∠ABC，且△ABC∽△BDC，
则∠A = °；
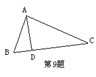9、如图，将①∠BAD =∠C，②∠ADB =∠
CAB，
③
，④
⑤
，
⑥
中的两个作为条件，另一个作为结论，
组成一个真命题，则条件是 ，结论是 ；（填序号即可）
10．如图,M是AC的中点，AB＝9，AC＝12，当AN＝ 时，△ABC∽△AMN．
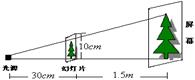
11．小华同学自制了一个简易幻灯机，其工作情况如图，则当幻灯片上小树的高度为10厘米时，屏幕上小树的高度是____________厘米。
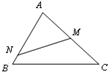
（10题图） （11题图）
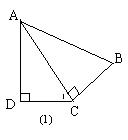
12.如图1,∠ADC=∠ACB=900,∠1=∠B,AC=5,AB=6,则AD=______.
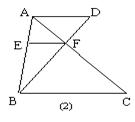
13.如图2,AD∥EF∥BC,则图的相似三角形共有_____对.
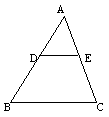
14. 如图，DE∥BC，AD＝15cm，BD＝20cm，则
___________。
15.两个相似三角形的面积之比为1∶5,小三角形的周长为4,则另一个三角形的周长为_____.
16. 命题“等角的补角相等”的条件是______________，结论是______________。
17.ΔABC的三边长为
,
,2,ΔA'B'C'的两边为1和
,若ΔABC∽ΔA'B'C',则ΔA'B'C'的笫三边长为________.
二、选择题（每空2分，共20分）
1、在比例尺为
的地图上，若，某建筑物在图上的面积为50 cm2，则该建筑物实际占地面积为（ ）
(A)、50 m2 (B)、5000 m2 (C)、50000 m2 (D)、500000 m2
2、下列两个图形，①两个等腰三角形，②两个直角三角形，③两个正方形，④两个矩形，⑤两个菱形，⑥两个正五边形，其中一定相似的有（ ）
(A)、2组 ( B)、3组
( C)、4组
(D)、5组
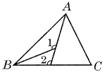
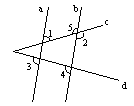
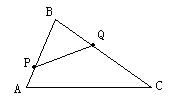
3、如图，∠C、∠1、∠2之间的大小关系是( )．
(A)、∠1<∠2<∠C (B)、∠2>∠1>∠C
(C)、∠C>∠1>∠2 (D)、∠1>∠2>∠C
4、如果一个三角形的两个外角的和是270°，则这个三角形一定是（ ）
(A)、锐角三角形 (B)、直角三角形 ( C)、钝角三角形 (D)、等腰三角形
5. 下列命题中真命题的个数是（ ）
（1）有一个锐角相等的两个直角三角形相似
（2）斜边和一直角边对应成比例的两个直角三角形相似
（3）任意两个矩形一定相似
（4）有一个内角相等的两个菱形相似
(A). 1个 (B). 2个 (C). 3个 (D). 4个
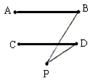
6. 已知：如图，AB∥CD，∠D＝38°，∠B＝80°，则∠P＝（ ）
(A). 52° (B).
42° (C).
10° (D).
40°
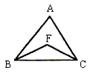
7.在△ABC中，BF、CF是角平分线，∠A＝70°，则∠BFC＝（ ）
(A). 125° (B). 110° (C). 100° (D). 150°
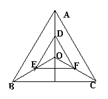
8．如图，点O是等边△ABC的中心，D、E、F分别是OA、OB、OC的中点，
则△DEF与△ABC是位似三角形，此时△DEF与△ABC的位似比，位似中心分别为（ ）
(A)．2、点B
(B)．
、点B (C)．2、点O (D)．、点O
9．如图，△ABC中，BD是∠ABC的平分线，DE∥AB交BC
于E，EC＝3，BE＝2，则AB＝（ ）
（A）．4 （B）．6 （C）．
（D）．
10.小正方形的边长为1，则下列图中的三角形与原图相似的是：（ ）
原图 （ A） （ B） （ C） （ D）
三. 作图题：（2分）
利用位似图形的方法把四边形ABCD放大2倍成四边形
。
四.证明题（每小题6分，共30分）
1. 已知∠1＋∠2＝180°，求证：∠3＝∠4。
2.已知如图，CD、CE分别是∠ADB、∠AEB的平分线，
求证：2∠C=∠A+∠B
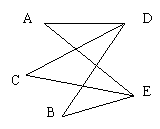
3．已知：如图，BE与CD交于点A，∠B＝∠D，
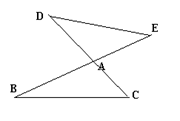求证：AB·DE＝AD·BC
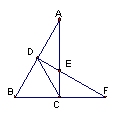
4.已知BD,CE是△ABC的高，
求证：① AD·AC=AE·AB
② ∠ADE=∠ABC
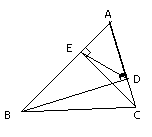
5．已知如图，CD是Rt△ABC斜边上的中线，DE⊥AB于D，交AC于点E，交BC的延长线于点F，
求证：①△DCE∽△DFC ② CD2=CE·CA
五.解答题（每小题8分，共64 分）
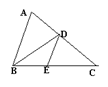
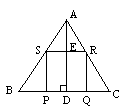
1.如图所示,在△ABC中,BC=60cm,高 AD=40cm,四边形PQRS是正方形.
(1). △ASR与△ABC相似吗?为什么?
(2).求正方形PQRS的面积。
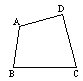
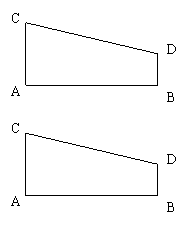
2．如图，直角梯形ABDC中，已知
，AB=7，AC=3，BD=2，在AB上找一点P，使以P、A、C为顶点的三角形与以P、B、D为顶点的三角形相似，求AP的长。
 |
3．已知如图，在△ABC中，AB = 8cm，BC = 16cm ，点P从点A出发沿AB边想向点B以2cm/s的速度移动，点Q从点B出发沿BC边向点C以4cm/s的速度移动，如果P、Q同时出发，经过几秒后△PBQ和△ABC相似？.
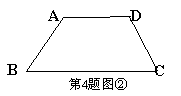
4、某生活小区的居民筹集资金1600元,计划在一块上、下底分别为10米,20米的梯形空地上种植花木如图①，（1）他们在△AMD和△BMC地带上种植太阳花,单价为8元/㎡，当△AMD地带种满花后（图中阴影部分）共花了160元,请计算种满△BMC地带所需费用.（2）若其余地带要种的有玫瑰和茉莉两种花木可供选择,单价分别为12元/㎡和10元/㎡，应选择哪种花木,刚好用完所筹集的资金.（3）若梯形ABCD为等腰梯形,面积不变（如图②）请你设计一种花坛图案,即在梯形内找到一点P,使得△APB≌△DPC,且S△APD=S△BPC，并说明你的理由.
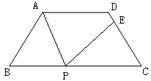
5、已知,梯形ABCD中,AD∥BC,AD<BC,且AD=5, AB=DC=2.（1）P为AD上一点,满足∠BPC=∠A,求证:△ABP∽△DPC；（2）如果点P在AD边上移动（P与点A、D不重合），且满足∠BPE=∠A,PE交直线BC于点E,同时交直线DC于点Q,那么,
当点Q在线段DC的延长线上时,设AP=x，CQ=y，求关于的函数解析式,并写出函数的定义域.
 | |||
 | |||
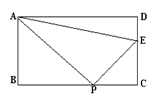6．如图：矩形ABCD中，BC＝12 cm，CD＝6
cm，
点P沿CB边从点C开始向点B以每秒2 cm的速度
移动，点E沿DC边从点D开始向点C以每秒1 cm
的速度移动，如果P、E同时出发，用t表示移动的
时间（0≤t≤6），
那么：⑴当t为何值时，△CPE为等腰三角形；
⑵当t为何值时，以C、P、E为顶点的三角形与△BAC相似。
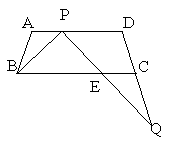
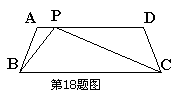
7.如图，等腰梯形ABCD中，
，
P为下底BC上一点（不与B、C重合），连结AP，过P点作PE交DC于E，
使得
。
（1）求证：
；
（2）求等腰梯形的腰AB的长；
（3）在底边BC上是否存在一点P，使得PE﹕EC=5﹕3 ? 如果存在,求BP的长;
如果不存在,请说明理由.
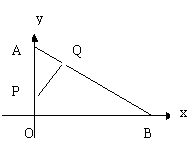
8．已知如图，在直角坐标系xoy中，点B(8,0)，点A(0,6),点P从点A出发沿AO向点O以1cm/s的速度移动，点Q从点B出发沿BA向点A以2cm/s的速度移动，如果P、Q同时出发，经过几秒后△PAQ和△ABO相似？并求直线PQ的解析表达式。.
 |