杭州外国语学校2005-2初二（下）期末考试数学试卷
命题人:刘 伟 审题人:顾彩梅
(本试卷总分100分、考试时间90分钟)
试卷说明:1、本试卷分试题卷和答题卷两部分,其中试题卷4页,答题卷4页,共4页;
2、本试卷共23小题,满分100分;3、请用蓝色(或黑色)钢笔(或圆珠笔)答题,除作图外不准用铅笔做答;4、答案一律填写在答题卷上,密封线内不要答题,考试结束后只上交答题卷.
一、 认真选择 (每小题3分,共20分)
1、 下列运算，（1）
，（2）
，（3）
，
（4）
，（5）
，其中正确的一共有 （ ）
A、2个 B、3个 C、4个 D、以上都不对
2、在下列下列各组根式中，是同类二次根式的是 （ ）
A、 
B、
C、
D、
3、甲、乙两人在相同的条件下各射靶10次，他们命中环数的平均数相同，但标准差不同，甲、乙的标准差分别为4， 5，则射击成绩比较稳定的是 （ ）
A、甲 B、乙 C、甲和乙一样稳定 D、以上都不对
4、
（
）
 |
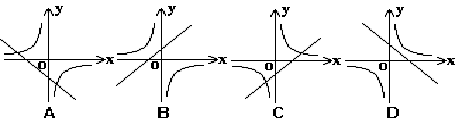5、如图所示，拦水坝的横断面为等腰梯形ABCD，已知：DC=3米，CE=2米，CB的坡度为1：
，则等腰梯形ABCD的周长是（单位：米）
（ ）
A、
B、8
C、
D、
 | |||
 | |||
（第5题图） (第6题图) (第8题图)
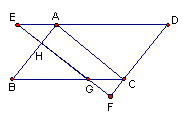
6、如图平行四边形ABCD中，EF∥AC，交DA以及DC延长线于点E、F，交AB与BC于
H、G，则图中与△AEH相似三角形（不包括全等）共有 （ ）
A、 4个 B、5个 C、6个 D、7个
7、已知一次函数
的图像平行，则一次函数
的图像不经过的象限是：
（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
8、如图，在不等边△ABC中，AB＞AC，AC≠BC，过AC上一点D作一条直线，使截得的三角形与原三角形相似，这样的直线可作 （ ）
A、2条 B、3条 C、4条 D、5条
9、已知数据1、2、3、3、4、5，则下列关于这组数据的说法错误的是： （ ）
A、平均数、中位数和众数都是3； B、极差为4；
C、方差为10；
D、标准差是
10、现有边长AB＝10，BC＝5的矩形纸片ABCD，对角线BD。在AB上取一点G，以DG为折痕，使DA落在DB上，则AG的长是： （ ）
A、
B、
C、
D、
二、精心填空(每小题3分,共15分)
11、计算：
=____________ .
12、函数
中，自变量x的取值范围是_________________.
13、在锐角△ABC中，如果有tanA＝2，则
________________.
14、如果
，那么k的值为___________________.
15、在△ABC中，若
，则∠C＝________.
三、细心计算（16题每小题4分，17题6分）
16、化简与计算：
（1）
（2）
17、在△ABC 中，∠B 、∠C 均为锐角，其对边分别为b、c,求证：
=
四、实际出发（18题5分,19题6分,共11分）
18、杭外初二共11个班组织活动，要从中选取2个班作为裁判。其中二（1）班是值日班必须作裁判，另外从二（2）班至二（11）班中选出一个班。二（3）班有同学建议用如下方法：从装有编号为1，2，3，4，5的五个白球的A袋中摸出一个球；再从装有编号为1，2，3，4，5，6的六个红球的B袋中再摸出一个（球除颜色外都一样），摸出的两球数字和是多少，就选几班，你认为公平吗？请说明理由。
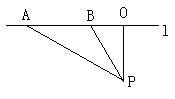
19、如图，已知测速站P到公路
的距离PO为40米，一辆汽车在公路上行驶，测得此车从A点行驶到B点所用时间为2秒，并测得
APO=
，计算此车从A到B的平均速度为每秒多少米？（结果保留三个有效数字）？并说明此车是否超过了每小时75千米的限度？
 |
五、好好理解（第20题5分，第21题7分，第22题8分，第23题10分）
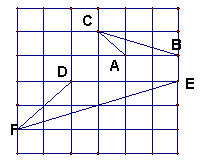
20、如图：在正方形网格上有△ABC，△DEF，它们相似吗？如果相似，说明理由并求出它们的相似比。
21、如图，直线
与两坐标轴分别相交于点A、B，作OD⊥AB于D。
（1） 写出A、B两点的坐标（用含b的代数式表示），并求tan∠OAB的值；
（2）
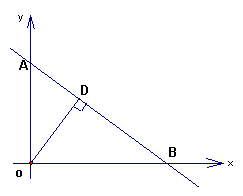如果AD＝
，求b的值。
22、如图，在等腰Rt△ABC中，∠A＝90°，D为斜边的中点。在DB上任取一点P，过P作两腰的垂线段PF、PE。连接EF。求证：
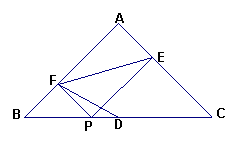
23、如图△ABC是一锐角三角形余料，边BC=16cm，高AD=24cm，要加工成矩形零件，使矩形的一边在BC上，其余两个顶点E、F分别在AB、AC上。
求：（1）AK为何值时，矩形EFGH是正方形？
（2）若设
，试写出
与
的函数解析式。
（3）为何值时，
达到最大值。
杭州外国语学校2005-2初二（下）期末考试数学试卷参考答案
一、 认真选择
1. A 2. C 3. A 4. D 5. C
6. A 7. A 8. C 9. C 10. C
二、 精心填空
11．
12．
13．
14．
或－1 15．
三、细心计算
16．（1） 
（2）
17．证明略
四、实际出发
18．解：判断是否公平的依据是2－11这几个数字出现的概率是否相同，若相同则方案公平，若出现概率不相同则方案不公平。可以发现2－11出现的几率分别为
，则此种方案是不公平的。
19．解：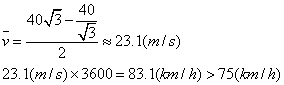
所以汽车超速。
五、好好理解
20．解：假设正方形网格的每个小正方形的边长是“1”，
则
三边分别为
，
三边分别为
。
，三边对应成比例，
，
21． （1） A(0,b) B(2b,0) b>0
(2) 
22．证明略
23．（1） 当
时，矩形EFGH为正方形；
（2）
；
（3）
当
时，
有最大值96。