吴江市2005－2006学年第二学期期末调研测试
初二数学
一、 选择题（本题共10个小题，每题3分，共30分，下面每小题给出的四个选项中，有且只有一个选项是正确的，请将正确选项的字母填在下面相应的表格中）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1、 若反比例函数
的图象在第二、四象限，则
的取值范围为
A、
B、
C、
D、
2、从放有3个红球、2个白球、1个黄球的袋中任意摸出1个恰好为白球的机会是
A、
B、
C、
D、
3、如图在ΔABC中，∠ACB=90°CD⊥AB，DE⊥AC，则图中与
ΔABC相似的三角形有
A、1个 B、2个
C、3个 D、4个
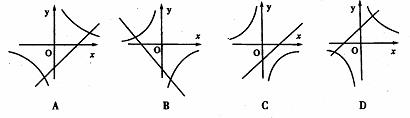
4、如图，函数
与
在同一坐标系中的图象只能是
5、如图，梯形ABCD的对角线相交于点O，有以下四个结论
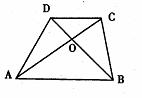①ΔAOB∽ΔCOD
②ΔAOD∽ΔACB
③
④
其中正确的有几个
A、1 B、2 C、3 D、4
5、某人沿着坡角为β的斜坡前进了50米，则他上升的高度是
A、
米 B、
米 C、
米 D、
米
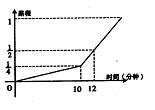6、一名考生前往考场，10分钟走了总路程的，估计步行不能
准时到达于是他改乘出租车赶往考场，他的行程与时间关系如图
所示，设总路程为1，则他到达考场所花的时间比一直步行提前
（假设该考生步行和乘车的速度都是均匀的）
A、20分钟 B、22分钟 C、24分钟 D、26分钟
8、一个等腰三角形的腰长等于一腰上的高的2倍，则这个等腰三角形的顶角为
A、30° B、120° C、30°或150° D、60°或120°
9、初二（1）班有48位学生春游前班长把全班学生对春游地点的意向绘制成扇形统计图，其中“想到苏州乐园的学生人数”的扇形圆心角为60°，则下列说法正确的是
A、想到苏州乐园的学生人占全班学生的60%；
B、想到苏州乐园的学生人有12人；
C、想到苏州乐园的学生人肯定最多；
D、想到苏州乐园的学生人占全班学生的。
10、应中共中央总书记胡锦涛同志的邀请，中国国民党主席连战先生、亲民党主席宋楚瑜先生，分别从台湾来大陆参观访问，先后来到西安都参观了新建成的“大唐芙蓉园”该园占地面积约为800000㎡，若按比例尺1：2000缩小后，其面积大约相当于
A、一个篮球场的面积；
B、一张乒乓球台台面的面积；
C、《吴江日报》的两个版面的面积；
D、《数学》课本封面的面积。
二、填空题（本题共10个小题，每题2分，共20分）
11、函数
中自变量x的取值范围是
。
12、双曲线
经过点
，则k=
。
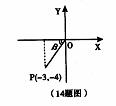
13、点
关于x轴对称点的坐标为
。
14、如图，
则
= 。
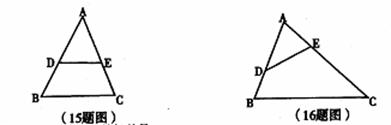
15、如图，DE//BC且AD=3，BD=2，BC=6，则DE= 。
16，如图，请增加一个条件： 使得ΔADE∽ΔACB。
17、一组数据3、7、9、15、4、8的极差是 。
18、邮购一种图书，每册定价20元，另加书价的5%作邮费购书x册需付款y（元），则y与x的函数关式为 。
19、已知，如图反比例函数
，点P是图象上任意一点，PM⊥x轴，PN⊥y轴，则四边形OMPN的面积为
。
20、如图在桌面上放置一个长方体，它的长、宽、高分别为4㎝、3㎝、2㎝，在顶点A处有一小昆虫沿长方体表面爬到顶点B，所爬的最短路程为 。
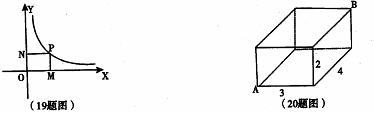
三、解答题（本大题共8小题，满分50分，解答时应写出必要的计算过程，推演步骤或文字说明）
21、计算（本题5分）tan30°·cos30°+
sin45°
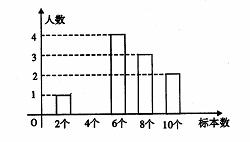
22、（本题6分）一个生物课外活动小组的同学举行植物标本制作比赛，结果统计如下表
| 人数 | 1 | 2 | 4 | 3 | 2 |
| 每人所作标本数 | 2 | 4 | 6 | 8 | 10 |
根据表中提供的信息，回答下列问题，
（1）该组共有学生 。
（2）所制标本的平均数 ，众数 ，中位数 。
（3）补全条形统计图。
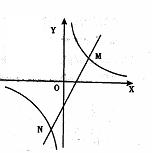23、（本题6分）如图一次函数
的图象与反比例函数的图象交于M
、N
两点。
（1）求这两个函数的解析式。
（2）根据图象写出使反比例函数值小于一次函数值时x的取值范围。
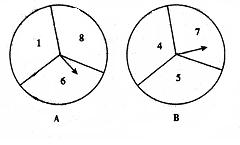
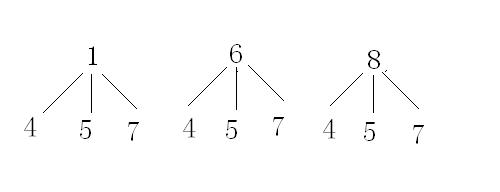
24、（本题6分）如图所示A、B两个转盘分别被三等分，转盘A上分别标有1，6，8，转盘B上分别标有4，5，7。现在小明和另一个同学分别用力转动转盘A、B的箭头，规定箭头所停区域的数字大的一方获胜（若箭头停在分界上则重新转动，直到箭头停在某一数字为止）那么你为小明选择一下，该选择哪个转盘获胜的可能性大，请画树状图说明理由。
 |
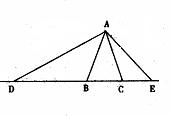
25、（本题6分）已知Rt△ABC中，AB=AC=5，∠BAC=40°，动点D、E分别在CB的延长线和BC的延长线上，且保持BD·CE=25，猜想∠DAE的大小是否会随着D、E的移动而发生变化？若不变，求出∠DAE的大小；若改变，试说明理由。
 |
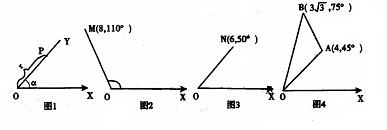
26、（本题7分）如图1将射线OX按逆时针方向旋转α角，得到射线OY，如果点P为射线OY上一点且OP=r，那么我们就规定用（r，α）表示点P在平面内的位置，并记为P（r，α），如图2中如果OM=8，∠XOM=110°，那么点M在平面内的位置记为M（8，110°），请解答下列问题：
（1）图3中如果点N在平面内的位置记为N（6，50°），那么ON= ，∠XON= 。
（2）图4中，如果点A、B在平面内的位置分别记为A（4，45°），B（
，75°）试求出点A、B的距离。
27、（本题7分）吴江市某工厂从2002年起开始投入技术改进资金，经技术改进后，其产品的生产成本不断降低，具体数据如下表
| 年度 | 2002 | 2003 | 2004 | 2005 |
| 投入技改资金x（万元） | 2.5 | 3 | 4 | 4.5 |
| 产品成本y（万元/件） | 7.2 | 6 | 4.5 | 4 |
（1） 请你认真分析表中数据，从你学过的一次函数和反比例函数中确定哪种函数能表示其变化规律，说明确定是哪种函数而不是另一种函数的理由，并求出它的解析式。
（2） 按照这种变化规律，若2006年已投入技改资金5万元
①、预计生产成本每件比2005年降低多少万元？
②、如果打算在2006年把每件成本降低到13.2万元，则还需投入技改资金多少万元？
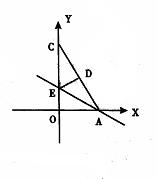
28、（本题7分）如图Rt△OAC是一张放在平面直角会标系中的三角形纸片，点O与原点重合，点A在x轴上，点C在y轴上，OA=
，∠CAO=60°，将Rt△OAC折叠使OA边落在AC边上，点O与点D重合，折痕为AE，
（1）求折痕AE所在直线的解析式；
（2）求点D的坐标；
（3）设点M为直线AE上的点，过点M作AC的平行线，交x轴于点N，是否存在这样的点M使得以M、N、D、A为顶点的四边形是平行四边形？若存在，请求出符合条件的点M的坐标。若不存在，请说明理由。
 |
吴江市2005－2006学年第二学期期末调研测试
初二数学参考答案
一、 选择题（本题共10个小题，每题3分，共30分，）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | C | D | A | C | B | C | C | D | C |
二、填空题（本题共10个小题，每题2分，共20分）
11、x≥1 12、
13、（2，3） 14、
15、
16、∠AEB=∠B等
17、12 18、y=21x(x为自然数) 19、2 20、
三、解答题（本大题共8小题，满分50分
21、原式=
………………………………（3分）
=
………………………………（4分）
=
………………………………（5分）
22、⑴、12 （1分）
⑵、6.5；6；6； (4分)
⑶ 略 (6分)
23、⑴、
、y=2x－2……………………（4分）
⑵、
或
…………………（6分）
24、应选择转盘A （1分）
转盘A出现的数字
转盘B出现的数字
结果 （1，4） （1，5）（1，7）（6，4）（6，5）（6，7）（8，4）（8，5）（8，7）
理由：对比结果，情况共有9种，其中A转出的数字转大的情况共有（6，4）、（6，5）、（8，4）、（8，5）、（8，7）5 种，所以选择A获胜的可能性为
，∴应选择转盘A（树状图对得4分，说明对得6分）
25、∠DAE的大小不会发生变化， （1分）
先证△ADB∽△EAC （4分）
再证出∠DAE=110° （6分）
26、⑴、6、50° （4分）
⑵、过A作AD⊥OB交OB于D，∠AOD=30° （5分）
AD=2，OD=
（6分）
BD= AB=
（7分）
27、⑴、若y与x是一次函数，则设y=kx+b，当x=2.5，时y=7.2；当x=3时,y=6代入上式得
∴
∴y=－2.4x+13.2.
验证，当x=4时，y=－2.4×4+13.2=3.6≠4.5；∴y与x不是一次函数
若y与x是反比例函数，则设
，同理求得
再验证……正确（能将其中一个函数说明正确得2分，二个函数都说明正确得3分）
⑵、①当x=5时，y=3.6（万元）……（4分）
成本降低：4－3.6=0.4（万元）……（5分）
②当y=3.2时，y=5.625 ……（6分）
还需投入：5.625－5=0.625（万元）……（7分）
28、⑴、
、E（0，1），直线AE：
………………（2分）
⑵AD=AO=，过点D作DF⊥x轴于F
AF=
DF= ∴OF=
∴D（，）…………………………………………（4分）
⑶、①过D作DM1 ∥x轴交AE于M1，作M1N1//AC交x轴于N1，∵D（，）
∴设M1（x1，）点M1在直线上求得M1（
，）；
②同理设M2（x2，－）求得
（求出一种情况得6分，求出两种情况得7分）