八年级下期期末考试

宜宾市翠屏区2004－2005学年下期期末检测

八年级数学试题

（全卷满分100分，120分钟完卷）

学号：　　　　  姓名：　　　　   成绩：　　　　

一、单项选择题：（每小题3分，共30分）

1、下列说法正确的是（　　）

A．　 无限小数是无理数　　　　　　　B．带根号的数是无理数

C．无理数是无限不循环小数　　　　 D．无理数是开方开不尽的数

2、一组数据共有50个，分为6组，第1—4组的频数分别为10，6，9，4．第5组占总数的10%，则第6组的频数为：(　　)

A．10　　　　B．12　　　　C．14　　　　 D．16

3、一个口袋中装有5个红球和4个白球，且它们的形状大小完全相同，从中一次性任取2个球，则下列事件发生的机会较大的是(　　)

A．两个红球　B．一红一白　C．两个白球　 D．一红一绿

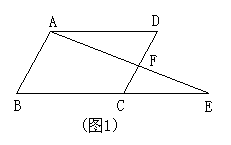
4、如图1，E是平行四边形ABCD的边BC

的延长线上的一点，连结AE交CD于F，则

图中共有相似三角形(　　)

A．1对　　 B．2对　

C．3对　　 D．4对

5、计算 的结果是 (　　 )

A．3.14–π　 B．–3.14+π　　 C．–3.14–π　　　D．3.14+π

6、在Rt△ABC中，∠C=90°，cosB= ，则sinB的值为 (　　)

A．　　  B．　　　　  C．　　　　  D． 　

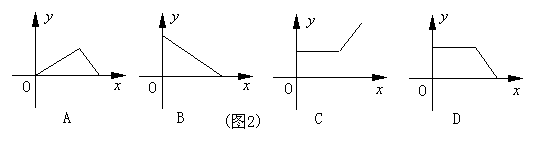7、开发区某消毒液生产厂家在2003年初，在库存m(m>0)的情况下，日销售量与产量持平，自4月底抗“非典”以来，消毒液要求量猛增，在生产能力不变的情况下，消毒液一度脱销，以下表示2003年初至脱销期间，时间 x 与库存量 y之间函数关系式的图象是 (　　)

8、下列函数中，y随x的增大而减少的函数是(　 )

A．y= –3x　　B．y= 4x　　C．y= – 　　 D．y=

9、如图4，沿倾斜角为30°的山坡植树，要求相邻两棵树之间的水平距离AC为2cm，那么相邻两棵树的斜坡距离AB为 (　　)

(精确到0.1m，可能用到的数据：≈1.73，≈1.41)

A．2.3　　 B．1.2　　　　 C．2.4　　　 D．不确定　　

10、如图5，P是△ABC的边BC异于B、C上任一点，过点P作直线截△ABC，使截得的三角形与△ABC相似，满足这样条件的直线共有(　　)

A．1条　　　　B．2条　　  C．3 条　　　D．4条　　

二、填空题：(每小题2分，共20分)

1、的平方根为　　　　　　 ．

2、数据2，2，3，4，4的方差S²=　　　　　  ．

3、函数y=的自变量x的取值范围是　　　　　　  ．

4、直线y= –2x+3不经过第　　　　  象限．

5、如图5，在平行四边形ABCD中，E为DC的中点，AE交BD于O，S_△ODE=12cm²，则

S_△ABO=　　　　　．

6、已知△ABC∽△A´B´C´且AB=2 A´B´，如果△ABC的周长是26cm，那么△A´B´C´的周长是　　　　　 ．

7、cot20°cotα=1，则∠α=　　　　  ．

8、点A(a+3，5) 和B (2，b–1)关于y轴对称，则(–a–b)²⁰⁰⁴=　　　　　 ．

9、直线y=2x–1与两坐标轴围成的三角形面积为　　　　　 

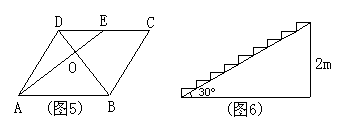10、如图6所示坡角为30°的楼梯表面上铺地毯，地毯的长度至少需要　　　　m ．(不取近似值)

三、计算：(每小题5分，共15分)

1、　　　　　　　　　　　　　　　　　   2、

3、

四、解答题(共35分)

1、  作图题(5分)

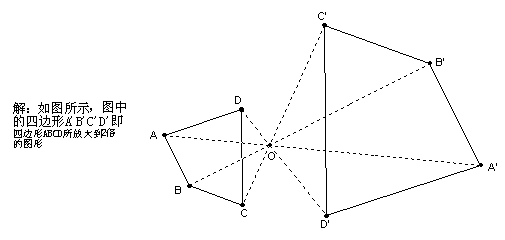
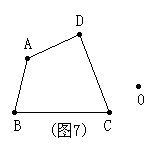利用位似图形的方法把如图所示的四边形放大到2倍成四边形A´B´C´D´．

2、(6分)已知某山区的平均气温与该山区的海拔高度的关系成一次函数，如下表：

海拔高度(单位：米)	0	100	200	300	400	……
平均气温(单位：°C)	22	21.5	21	20.5	20	……

(1)　  若平均气温用(°C)表示，海拔高度用(米)表示，试写出它们之间的函数关系式；

(2)　  若某种植物适宜生长在18°C~20°C(包含18°C，也包含20°C)山区，请问该植物适宜种植在海拔多少米的山区？

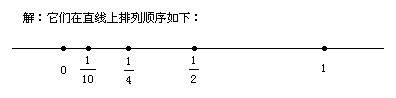
3、(5分)将下列事件发生的机会从小到大排列后的顺序表示在给出的直线上．

(1)　  在1—100中产生一个随机整数末尾恰好是偶数；

(2)　  从一副扑克牌中随意抽出一张恰好是5的整数；

(3)　  抛掷两枚硬币恰好出现2个正面；

(4)　  抛掷一枚普通的正方体骰子点数大于6；

(5)　  从装有1 个红球和2个黄球的黑袋中摸出一个恰好不是白球

4、(5分)如图8，点C、D在线段AB上，△PCD是等边三角形．

(1)　　当AC、CD、DB满足怎样的关系时，△ACP∽△PDB？

(2)　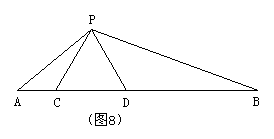　当△ACP∽△PDB时，求∠APB．

5、(5分)某校准备让甲、乙两家公司为毕业班学生制作一批纪念册，甲公司提出：每册收材料费5元，另收设计费1500元；乙公司提出：每册收材料费8元，不收设计费．

(1)　　请分别写出制作纪念册的册数x数与甲公司收费y₁与乙公司收费y₂的函数关系；

(2)　　若学校派你去甲、乙两家公司订做纪念册，你会选择哪家公司？

6、(4分)探索：如图9，在直角坐标系中，第一次将△OAB变成△OA₁B₁，第二次将△OA₁B₁变换成△OA₂B₂，第三次将△OA₂B₂变换成△OA₃B₃

已知：A(1，3)、A₁(2，3)、A₂(4，3)、A₃(8，3)

　　　B(2，0)、B₁(4，0)、B₂(8，0)、B₃(16，0)

(1)　　观察每次变化前后的三角形有何变换，找出规律，按此变换规律再将△OA₃B₃变换成

△A₄B₄，则A₄的坐标是　　　　  ，B₄的坐标是　　　　　

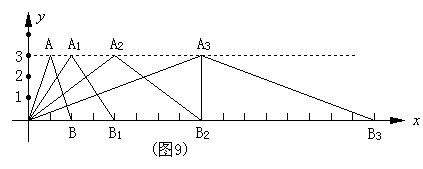(2)若按(1)题找到的规律将△OAB进行n次变换，得到△OA_nB_n，比较每次变化中三角形顶点坐标有何有何变化，找出规律，推测A_n的坐标是　　　　　 ，B_n的坐标是　　　　 

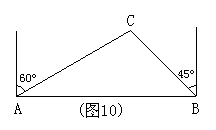7、(本小题5分)如图10，去年某省将地处A、B两地的两所大学合并成一所综合性大学，为了方便A、B两地师生的交往，学校准备在相距2千米的A、B两地之间修筑一条笔直的公路(即图中线段AB)，经测量，在A地的北偏东60°方向，B地的西偏北45°方向C处有一个半径为0.7千米的公园，问计划修筑的这条公路会不会穿过公园？

宜宾市翠屏区2004－2005学年下期期末检测

八年级数学试题

　　　　　　　　　　　　　　　　　  　　（参考答案）

学号：　　　　  姓名：　　　　   成绩：　　　　

一、单项选择题：（每小题3分，共30分）

1．C　2．D　3．B　4．C　5．B　6．B　7．D　8．A　9．A　10．D

二、填空题

1．±3　2．0.8 ( ) 3．x≥–1　4．三　5．48cm²　6．13cm　7．70°　8．1　9．　10．（2+2）

三、计算：

1．5　　  2．30　　 3．

四、解答题

1、作图题

2．(1) y= –0.005x+22

(2)　  400m~800m之间

3．

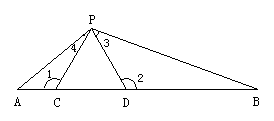4．解：(1)当CD² =AC·BD时，△ACP∽△PDB，理由如下：

∵△PCD是等边三角形

∴∠PCD =∠PDC=60°

　 CD=PC=PD

∵∠1=180°–∠PCD

∴∠1=120°

同理，∠2=120°

　　∴∠1=∠2

　　∵CD² =AC·BD

　　∴ =

又∵CD =PC= PD

　∴ =

5、(1)　y₁=5x+1500 (x≥0)　　 y₂=8x (x≥0)

　 (2)　当x＞500，选甲家公司

　　　 当x = 500,两家公司任选一家

　　　 当x＜500，选乙家公司

6、(1) (16,3)　 (32,0)　　(2) (2ⁿ,3)　(2ⁿ⁺¹,0 )

7、过C点作CD⊥AB，垂足为D

　　CD=-1≈0.732＞0.7, ∴计划修筑的这条公路不会穿过公园

试题录入者：宜宾市李庄中学：况永胜　联系：　电话：