八年级数学上期末模拟测试
姓名__________ 班级__________ 分数__________
A卷（100分）
一、选择题（8×3′=24′）
1、下列各数中，有理数的个数为( )
;
; 0.53; 
;
0 ; 
;
;
A.3个 B.4个 C.5个 D.6个
2、三峡工程在6月1日于6月10日下闸蓄水期间，水库水位由106米升至135米，高峡平湖初现人间，假设水库水位匀速上升，那么下列图象中，能正确反映这10天水位h（米）随时间t（天）变化的是（ ）
135
135
135
135
106 106 106 106
0 t(天) 0 t(天) 0 t(天) 0 t(天)
A .B .C. D.
3、下列几个图案是生活中的一些标志，其中既是轴对称图形又是中心对称图形的有几个
A.0个 B.1个 C.2个 D.3个
4、已知 
,
,
，则a、b、c的大小关系为（ ）
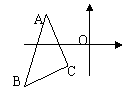A.a<b<c
B.a>b>c
C.a<c<b
D.b<a<c
5、将△ABC的三个项点坐标的横坐标乘以-1，纵坐标不变，
则所得图形与原图的关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.将原图的x轴的负方向平移了了1个单位
6、如图，小强和妈妈买了一个竹竿，不料坐电梯（其内部形如长方体）
回家时遇到了麻烦，如果电梯内部的长、宽、高分别是1.5米、1.5米、
2.2米，要使小强和妈妈买的竹竿能顺利地带回家中，
竹竿最长只能买（ ）米长。
A.2.8米 B.2.9米
C.3.0米 D.3.1米
7. 已知正比例函数
（
）的函数值
随
的增大而增大，则一次函数
的图象大致是
[ ]
A
B
C
D
8.如果方程组
的解是方程
的解, 那么
的值是
[ ]
A. 20 B. -15 C. -10 D.5
二、填空题：将答案填写在答题框指定的位置（每小题3分，共24分）
1、已知三角形的三边长为5、12、13，则此三角形的面积为 。
2. 的相反数是 , 其倒数是 ,(
)的绝对值是 .
3、点M（3，a）在直线y=-x上，若点M向右平移3个单位得点N, 则N点坐标是
4、小明在一个学期的数学测试成绩如下：
| 单元1 | 单元2 | 单元3 | 期中 | 期末 |
| 84 | 90 | 78 | 90 | 87 |
如果平时成绩按3次单元平均成绩计，学期成绩按平时、期中、期末各占30%、30%和40%计，小明的数学成绩是 分
5、如图，AD、AE是正六边形的两条对角线，不添加任何辅助线，请写出两个正确的结论：（1）
；
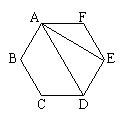（2）
______________。
（只写出两个你认为正确的结论即可）
6.棱形的两条对角线长分别为6
和10,其周长
.
7.多边形的内角和与某个外角的度数总和为1350，则多边形的边数为 .
8. 汽车开始行驶时，油箱中有油30升，如果每小时耗油4升，
那么油箱中的剩余油量y(升)和工作时间x（时）之间的函数关系式是 .
三、计算题（每小题4分，共16分）
1、计算： （1）、
（2）、
2、解方程：（1）、
（2）
（用图象法）
四、解答题
1．（6分）如图，正方形纸片ABCD的BC边上有一点E，AE=10㎝．若把纸片沿AE的中垂线折叠，使点E与点A重合，你能求出纸片上折痕MN的长吗？解释你的方法．
 |
2、（6分）八年级某班教室里，三位同学正在为谁的数学成绩最好而争论，他们的五次数学成绩如表1所示，这五次数学成绩的平均数、中位数、众数如表2所示
| 学生姓名 | 数学成绩 | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 小芳 | 97 | 93 | 94 | 61 | 97 |
| 小林 | 61 | 61 | 97 | 98 | 99 |
| 小军 | 98 | 98 | 84 | 61 | 39 |
| 学生姓名 | 平均数 | 中位数 | 众数 |
| 小芳 | 88.4 | 94 | 97 |
| 小林 | 83.2 | 97 | 61 |
| 小军 | 76 | 84 | 98 |
现在这三位同学都说自己的数学成绩是最好的。
（1）请你猜测并写出他们各自的理由；（3分）
（2）三人似乎都有道理，你对此何看法？请运用统计知识作出分析。（3分）
| |
3.（8分）如图,表示名湖商场一天的彩电销售额与
销售量的关系,表示该公司一天的销售成本与
彩电销售量的关系.
①时,销售额= 万元,销售成本=
万元.利润(收入- 成本)= 万元.
②一天销售 件时,销售额等于销售成本.
③对应的函数表达式是 .
④写出利润与销售量间的函数表达式.
4、（8′）用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合，使三角尺的60°角的顶点与点A重合，两边分别与AB，AC重合.将三角尺绕点A按逆时针方向旋转.
（1）当三角尺的两边分别与菱形的两边BC，CD相交于点E，F时，（如图13—1），通过观察或测量BE，CF的长度，你能得出什么结论？并证明你的结论；
（2）当三角尺的两边分别与菱形的两边BC，CD的延长线相交于点E，F时（如图13—2），你在（1）中得到的结论还成立吗？简要说明理由.
5、（8′）甲、乙两件服装的成本共500元,商店老板为了获取利润,决定将甲服装按50%的利润定价, 乙服装按40%的利润定价,在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两种服装的成本各是多少元?
B卷（50分）
一、填空题（18分）
1、已知点A（2，0）和直线y=-x+3上一点P,若S△AOP=4，则点P的坐标为_________.
2、解方程组时,甲正确解得,乙因看错了c，而求得，则a+b+c=________________.
3、如图，已知图中每个小方格的边长为1，则点C到AB所在直线的距离等于 。
4、如图,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线上的一个动点,则PE+PB和最小值为________________.
5、下面是用棋子摆成的“上”字：
第一个“上”字 第二个“上”字
第三个“上”字
如果按照以上规律继续摆下去，那么通过观察，可以发现：
（1）第四、第五个“上”字分别需用 和
枚棋子；（2分）
（2）第n个“上”字需用
枚棋子．（1分）
6、如图，是一块电脑屏幕上出现的距形色块，由6块颜色不同
的正方形组成，设中间最小一个正方形的边长为1，
则这个距形面积是 。
二、解答题
1、(本题满分6分)已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请证明,若不正确请举反例说明;
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
2、（8分）某商场计划从厂家购进电视机,已知该厂生产三种不同型号的电视机,出厂价格分别是甲种每台1500元, 乙种每台2100元, 丙种每台2500元,（1）若商场同时购进其中两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案.（2）已知商场销售一台甲型电视机可获利150元, 售一台乙型电视机可获利200元, 售一台丙型电视机可获利250元,在（1）的方案中为使销售时获利最多,应该选择哪种进货方案?
3、（8分）如图，△ABC中，点O是AC边上一动点，过点O作直线MN‖BC,设MN交∠BCA的平分线于E，交∠BCA的外角平分线于点F。
（1） 说明：EO＝OF
（2） 当点O运动到何处时，四边形AECF是距形？并说明理由。
（3） 当△ABC满足什么条件时，四边形AECF是正方形？并说明理由。
4、（10分）如图15—1和15—2，在20×20的等距网格（每格的宽和高均是1个单位长）中，Rt△ABC从点A与点M重合的位置开始，以每秒1个单位长的速度先向下平移，当BC边与网的底部重合时，继续同样的速度向右平移，当点C与点P重合时，Rt△ABC停止移动.设运动时间为x秒，△QAC的面积为y.
（1）如图15—1，当Rt△ABC向下平移到Rt△A1B1C1的位置时，请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形；
（2）如图15—2，在Rt△ABC向下平移的过程中，请你求出y与x的函数关系式，并说明当x分别取何值时，y取得最大值和最小值？最大值和最小值分别是多少？
（3）在Rt△ABC向右平移的过程中，请你说明当x取何值时，y取得最大值和最小值？最大值和最值分别是多少？为什么？