希望杯全国联赛试卷

第十六届“希望杯”全国数学邀请赛

得分

初二　第2试

2005年4月17日　　上午8∶30至10∶30

一、选择题（每小题5分，共50分）以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母填在每题后面的圆括号内.

1、若a，b均为正整数，m=ab(a＋b)，则（　　）

A．m一定是奇数　　　　　　　　　　  B．m一定是偶数　　　

C．只有当a，b均为偶数时，m是偶数　 D．只有当a，b一个为偶数，另一个为奇数时，m是偶数

2、设，，则等于（　　）

A．　　　　　　　 B．－　　　　　　 C．－3　　　　　　　  D．3

3、Given a，b，c are positive integers，and a，b are prime numbers，，then the value of  is（　　）

A．14　　　　　　　  B．13　　　　　　　 C．12　　　　　　　  D． 11

(英汉词典 positive integers：正整数. prime numbers：质数)_

4、购买铅笔7支，作业本3个，圆珠笔1支共需3元；购买铅笔10支，作业本4个，圆珠笔1支共需4元，则购买铅笔11支，作业本5个，圆珠笔2支共需（　　）

A．4.5元　　　 　　　B．5元　　　　　　 C．6元　　　　　　　 D．6.5元

5、计算机将信息转换成二进制数来处理.二进制是“逢二进一”，如二进制数(1101)₂转换成十进制数是1×2³＋1×2²＋0×2¹＋1×2⁰=13，那么二进制数转换成十进制数是（　　 ）

A．2²⁰⁰⁴＋1　　　　　 B．2²⁰⁰⁵　　　　　　 C．2²⁰⁰⁵－1　　　　　　 D．2²⁰⁰⁵＋1　

6、已知△ABC的三个内角的比是m∶(m＋1) ∶(m＋2)，其中是m大于1的正整数，那么△ABC是（　 ）

A．锐角三角形　　　 B．直角三角形　　　 C．钝角三角形　　　　  D．等腰三角形

7、已知△ABC的三条高的比是3∶4∶5，且三条边的长均为整数，则△ABC的边长可能是（　　 ）

A．10　　　　　　　 B．12　　　　　　　 C．14　　　　　　　　  D．16

8、已知两位数能被3整除，它的十位数字与个位数字的乘积等于它的个位数字，且它的任意次幂的个位数字等于它的个位数字。这样的两位数共有（　　）

A．1个　　　　　　 B．3个　　　　　　  C．4个　　　　　　　  D．5个

9、放成一排的2005个盒子中共有4010个小球，其中最左端的盒子中放了a个小球，最右端的盒子中放了b个小球，如果任何相邻的12个盒子中的小球共有24个，则（　　）

A．a=b=2　　　　　 B．a=b=1　　　　　  C．a=1，b=2　　　　　 D．a=2，b=1

10、已知整数，，满足≤＜，且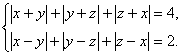那么x²＋y²＋z²的值等于（　 ）

A．2　　　　　　　 B．14　　　　　　　  C．2或14　　　　　 　 D．14或17

二、填空题（每小题5分，共50分.含两个空的小题，前空3分，后空2分.）

11、如果a=3，b=5，那么a＋b－a－b的绝对值等于　　　　　　　　  .

12、已知，则=　　　　　　　　　  .

13、某汽车从A地驶向B地，若每分钟行驶a千米，则11点到达，若每分钟行驶a千米，则11∶20时距离B地还有10千米；如果改变出发时间，若每分钟行驶a千米，则11点到达，若每分钟行驶a千米，则11∶20时已经超过B地30千米。A、B两地的路程是　　　　　　　 千米。

14、若是一个六位数，其中a，b，c是三个互异的数字，且都不等于0，1，2，3，又M是7的倍数，那么M的最小值是　　　　　　　　　　 .

15、分解因式：　　　　　  　　　　　　　 .

16、若在凸n(n为大于3的自然数)边形的内角中，最多有M个锐角，最少有m个锐角，则M=　　　　；

m=　　　　　　 .

17、如图1，等腰Rt△ABC的直角边长为32，从直角顶点A作斜边BC的垂线交BC于D₁，再从D₁作D₁D₂⊥AC交AC于D₂，再从D₂作D₂D₃⊥BC交BC于D₃，…，则AD₁＋D₂D₃＋D₄D₅＋D₆D₇＋D₈D₉=　　

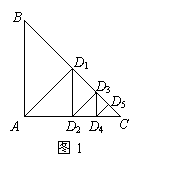　　　 ；D₁D₂＋D₃D₄＋D₅D₆＋D₇D₈＋D₉D₁₀=　　　　　　　　  　 .

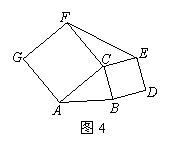
18、如图2，将三角形纸片ABC沿EF折叠可得图3(其中EF∥BC)，已知图3的面积与原三角形的面积之比为3∶4，且阴影部分的面积为8平方厘米，则原三角形面积为　　　　　　　　  平方厘米。

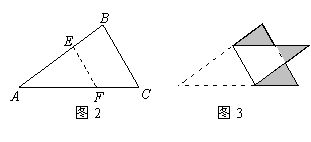
19、如图4，△ABC中，BC∶AC=3∶5，四边形BDEC和ACFG均为正方形，已知△ABC与正方形BDEC的面积比是3∶5，那么△CEF与整个图形的面积比等于　　　　　　　　 .

20、如果正整数n有以下性质：n的八分之一是平方数，n的九分之一是立方数，它的二十五分之一是五次方数，那么n就称为“希望数”，则最小的希望数是　　　　　　　　　  .

三、解答题（每题10分，共30分） 要求：写出推算过程.

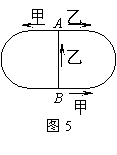
21、图5是一个长为400米的环形跑道，其中A、B为跑道对称轴上的两点，

且A、B之间有一条50米的直线通道。甲、乙两人同时从A点出发，甲按

逆时针方向以速度v₁沿跑道跑步，当跑到B点处时继续沿跑道前进，乙按

顺时针方向以速度v₂沿跑道跑步，当跑到B点处时沿直线通道跑回A点处。

假设两人跑步时间足够长。求：

⑴如果v₁∶v₂=3∶2，那么甲跑了多少路程后，两人首次在A点处相遇？

⑵如果v₁∶v₂=5∶6，那么乙跑了多少路程后，两人首次在B点处相遇？

22、⑴如果a是小于20的质数，且可化为一个循环小数，那么a的取值有哪几个？

⑵如果a是小于20的合数，且可化为一个循环小数，那么a的取值有哪几个？

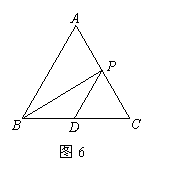23、如图6，正三角形ABC的边长为a，D是BC的中点，P是AC边上的点，连结PB和PD得到△PBD。求：

⑴当点P运动到AC的中点时，△PBD的周长；

⑵△PBD的周长的最小值。

第十六届“希望杯”全国数学邀请赛

参考答案及评分标准

初中二年级 第2试

一、选择题（每小题5分）　　　　　　　　　　 

题号	1	2	3	4	5	6	7	8	9	10
答案	B	C	D	B	C	A	B	C	A	A

二、填空题（每小题5分，含两个空的小题，前空3分，后空2分）　　　　　　　　　　　　 

　　　　　　　　　　　 

题号	11	12	13	14	15	16	17	18	19	20
答案	6		54	468321		3；0	31；31	16		215·320·512

三、解答题

21、⑴设甲跑了n圈后，两人首次在A点处相遇，再设甲、乙两人的速度分别为v₁=3m，v₂=2m，

由题意可得在A处相遇时，他们跑步的时间是　　　　　　　　 （2分）

是　　　　　　　　　　　　　　　　  （3分）

因为乙跑回到A点处，所以应是250的整数倍，从而知n的最小值是15，（4分）

所以甲跑了15圈后，两人首次在A点处相遇　　　　　　　　　　　　  （5分）

⑵设乙跑了米，甲跑了米时，两人首次在B点处相遇，设甲、乙两人的速度分别为v₁=5m，v₂=6m，由题意可得，即 ，　　 （7分）

所以，即(p，q均为正整数)。

所以p，q的最小值为q=2，p=4，　　　　　　　　　　　　　　　　　　  （8分）

此时，乙跑过的路程为250×4＋200=1200（米）。　　　　　　　　　　　　 （9分）

所以乙跑了1200米后，两人首次在B点处相遇。　　　　　　　　　　　　 （10分）

22、⑴小于20的质数有2，3，5，7，11，13，17，19　　　　　　　　　　 （2分）

除了2和5以外，其余各数的倒数均可化为循环小数，　　　　　　　　　　 （4分）

所以a可以取：3，5，7，11，13，17，19。　　　　　　　　　　　　　　  （5分）

⑵由⑴可知，只要合数a的因数中含有2或5以外的质数，那么该数的倒数均可化为循环小数，（8分）

所以a可以取：6，9，12，14，15，18。　　　　　　　　　　　　　　　　  （10分）

23、⑴如图1，当点P运动到AC的中点时，BP⊥AC，DP∥AB，　　　　　  （2分）

所以 ，，，　　　　　　　　　　　 　　　（4分）

即△ABC的周长为BP＋DP＋BD=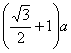。　　　　　　　　　　　　　  （5分）

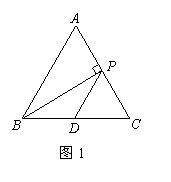⑵如图2，作点B关于AC的对称点E，连结EP、EB、ED、EC，则PB＋PD=PE＋PD，因此ED的长就是PB＋PD的最小值，即当点P运动到ED与AC的交点G时，△PBD的周长最小。　　　 （7分）

从点D作DF⊥BE，垂足为F，因为BC=a，所以，。

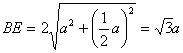因为∠DBF=30°，所以，，

，。　　　　　　　　　　　　　　 （9分）

所以△PBD的周长的最小值是。　　　　　　　　　　　　　　　  （10分）