上虞市2004学年第一学期八年级期末学业评估卷
数 学
(时间90分钟,满分100分)
| 题号 | 一 | 二 | 三 | 总分 | ||||||
| 1-10 | 11-20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | ||
| 得分 | ||||||||||
| 评卷人 | ||||||||||
同学们：每个人都要经过许多的考验，今天我们就面对一次小小的考验，相信自己，努力争取，我们每一个人都能成功！
关心你的数学老师
一、请你填一填，可要小心哦！（本大题有10小题，第4题4分，其余每题2分，共22分）
1．用不等式表示：a的2倍与4的差是正数___________，并写出满足不等式条件的一个数___________.
2．在你所了解的图形中， 是中心对称图形.（写出2个即可）
3．抛掷一枚一元硬币，出现国徽一面向上的机会是
．
4．如图，△ABC为等边三角形，边长为2cm，D为BC中点，△AEB是△ADC 绕点A旋转60°得到的，则∠ABE＝_______度；BE＝______cm．若连结DE，则△ADE为__________三角形．
5．小芳第一次数学测验得80分，第二次得86分，则当第三次得
分x 分时，才能使三次的平均成绩不低于85分.
6．不等式5x-2＜3(x+6)的解是 .
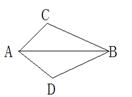
7．如图，已知AC=AD，若要使ΔABC通过翻折能与ΔABD重合，请你补充条件
.（只需填写一个你认为适当的条件）
8．如图，把一个长方形纸片沿EF折叠后，点D、C分别在D′、C′位置，若∠EFB=65°，则∠AED′=_________.
9．已知菱形ABCD中，若它的面积是12，且AC=3，则BD=___________.
10.木工师傅用两根相等的长木条及两根相等的短木条制作了一个门框，如图，现 在给你一条足够长的绳子，请你说出根据
,可以验证这个门框的形状恰好是一个矩形.
二、请你选一选，可要仔细呀！（本大题有10小题，每小题3分，共30分）
11．下列计算结果是a8的是（ ）
A.a2·a4 B.a4+a4 C.(a2)4 D.2a4
12．△ABC沿水平方向平移到△A′B′C′，若AA′=5，则BB′等于（ ）
A．
B.5
C.10 D.20
13．
，则下列各式中成立的是（ ）
A. 
B. 
C. 
D. 
14．下列说法中正确的是（ ）
A．实验是预测机会大小的一种方法;
B．掷瓶盖出现正面的机会与抛掷硬币出现正面的机会相等;
C．掷两枚普通骰子，出现点数之和为5的机会为 
;
D．抛掷硬币的实验中，如果没有硬币，可用图钉替代.
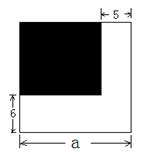
15．如图，一块正方形铁皮，边长为a，如果一边截去6，另一边截去5，则所剩长方形铁皮的面积（阴影部分）是：
①（a-5）(a-6)； ② a2-5a-6(a-5)；③ a2-6a-5(a-6)；④ a2-5a-6a+30；
以上答案中，正确的有（ ）
A．4个 B．3个 C．2个 D．1个
16. 
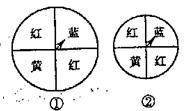如图，是两个用来摇奖的转盘，几位同学的说法中，其中正确的是（ ）
A．小王说：转盘①中蓝色区域的面积比转盘②中的蓝色区域面积要大，所以摇转盘①比摇转盘②时，蓝色区域得奖的可能性较大
B．李兵说：两个转盘中指针指向蓝色区域的机会一样大
C．在转盘①中，指针指向红色区域的频率是
D．在转盘②中只有红、黄、蓝三种颜色，指针指向每种颜色的机会都是.
17.三张反面相同的卡片,正面分别写着“木，木，寸”，把它们洗匀，反面朝上任取两张，则能拼成文字“村”的机会是（ ）
A． B．
C．
D．
18．已知（x-y）2=18,xy=20,则（x+y）2=( )
A.98 B.78 C.58 D.38
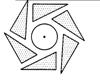19.
如图是一个旋转对称图形，要使它旋转后与自身重合，至少应将它绕中心逆时针方向旋转的度数是（ ）
A.30° B. 60° C.120° D.180°
20．利民水果店进了某种水果1吨，进价为6元/千克，出售价为10元/千克，销去一半后，为尽快售完，水果店准备打折出售，如果要使总利润不低于3000元，那么余下的水果最多可按原定价的（ ）折出售.
A.7.5折 B.8折 C.8.5折 D.9折
三、请你解一解，可要耐心啊！（本大题满分48分）
21.（本题8分）计算下列各题:
(1)(a-3b)2-(3a-b)2 (2)(x+3)(x-4)-(x-1)2
22. （本题8分）把下列多项式分解因式:
(1) x3-25x (2) 4x3y+4x2y2+xy3
23.（本题6分）解下列不等式组,将解集在数轴上表示出来,并求出符合条件的整数解.
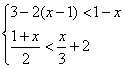
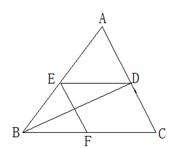24．（本题6分）如图，ΔABC中，BD平分∠ABC，DE∥BC，EF∥AC，试确定CF与BE的大小关系，并说明理由.
25．(本题6分)小聪与小明在掷一枚质量均匀的骰子，他们规定只掷一次，小聪说：“若你掷到点数是6，你赢，否则我赢．”而小明说：“不，若你掷到的点数是1或2中的一种，那你赢，否则是我赢．”
问：（1）你认为他们的规则对两人公平吗？请说明理由；
（2）请你设计一种方案，在其他条件不变的情况下，使两人赢的机会均等．
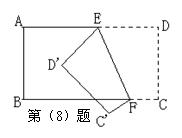
26．（本题6分）请仔细观察图A和图B，解答下列问题：
⑴ 请简述由图A变换为图B的形成过程.
⑵ 若AD=3，DB=4，求△ADE与△BDF面积的和.
27． (本题8分)实践探索题：
（1）拼一拼，画一画：
| |
| |
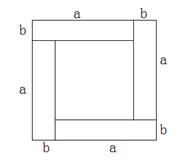
（3）当拼成的这个大正方形边长比中间小正方形边长多3cm时，它的面积就多24cm2，求中间小正方形的边长.
参考答案及评分意见
一、填空题（本大题有10小题，第4题4分，按2、1、1计，其余每题2分，共22分）
1.2
-4>0, 如3； 2.平行四边形和菱形（其它如正方形，圆等）； 3. 50%；
4.60，1，等边（或正）； 5.x≥89（无等号扣1分）； 6.x<10；
7.BC=BD或∠CAB=∠DAB； 8. 500； 9. 8； 10.对角线相等的平行四边形是矩形.
二、选择题（每小题3分，共30分）
11．C 12.B 13.D 14. A 15.A 16.B 17. B 18.A 19.B 20.B
三、解答题（共48分）
21．（每项正确得1分，结果正确得2分）（1）-8a2+8b2； (2)x-13．
22.（分解一次正确得２分）(1)x(x+5)(x-5)； (2)xy(2x+y)2．
23.每个不等式的解正确得１分，写出结果4<x<9得1分；在数轴上表示正确得２分；整数解为5，6，7，8. （1分）
24.写出CF=BE（２分）,理由如下: ∵BD平分∠ABC, ∴∠ABD=∠DBC,
∵DE∥BC, ∴∠EDB=∠DBC, ∴∠ABD=∠EDB, ∴EB=ED, （２分）
又∵EF∥AC,DE∥BC, ∴四边形EFCD是平行四边形,
∴ED=FC, （２分） ∴EB=CF.
25.(1)他们的游戏不公平（１分）.理由是:小明成功的机会是
,
而小聪成功的机会是,小聪获胜的机会大于小明获胜的机会,因此不公平. （２分）
(2)只要规定只掷一次,若掷出的点数为奇数,则规定小聪获胜；
若掷出的点数为偶数,则规定小明获胜．（２分）
这样两人成功的机会各占一半, （１分）故游戏公平.
26．（1）图A中△A1DF绕点D顺时针方向旋转90度得图B（3分）
（2）图B中△ADE与△BDF面积的和即为图A中△A1DB的面积，由旋转知∠A1DB=90°，A1D=AD=3（2分），所以△A1DB面积为6，即△ADE与△BDF面积的和为6（1分）
27.(1)拼出草图见左面: （2分）
(2)方法1:(a+b)2-4ab=a2+2ab+b2-4ab=a2-2ab+b2；（1分）
方法2:(a-b)2=a2-2ab+b2；（1分）
发现:(a+b)2-4ab=(a-b)2. （1分）
(3)根据题意得: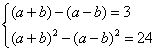 
解得:
（1分）
故a-b=4-
=
cm,
答:中间小正方形的边长是cm. （1分）