2006年春石狮市中英文学校八年级数学竞赛试卷
（本卷分A、B、C三个等级卷：A卷属轻松答题卷，B卷属会做答题卷，C卷属探索答题卷.满分150分，答卷时间共120分钟.命题：卢范龙）
班级____ 姓名__________ 座号_____ 成绩__________
A卷(50分)
一、填空题(每小题2分,共20分)
1. 4的平方根是_____.
2.
=____.
3.函数y=
自变量取值范围是_____________.
4.点A(2,-3)关于y轴的对称点是______.
5.直线y=2x+2与y轴的交点是________.
6.反比例函数的图象过点(1, 1),则此反比例函数的解析式是__________________.
7.若某地图的比例尺为1:, A,B两地的实际距离为400km,则该地图上A,B两地的距离是_____.
8. Rt△ABC, ∠C=90°如图,AC=8,AB=10,则边BC=______.
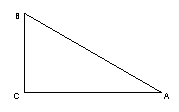
9.Rt△ABC中,∠C=90°,a=3b,则tanA=_____.
10.一组数据4,6,3,7,5的方差是_____.
二、选择题(每小题3分,共9分)
11．下列不是同类二次根式的一组是( )
A．
与
B．
与
C．
与
D．
与
12. 下列叙述正确的是( )
A．y=
中y随x的增大而减小.
B．直线y=-2x可由y=-2x-1沿着y轴向下平移1个单位的长度而得
C．相似三角形是全等的三角形的特例.
D．口袋中有1个红球和2个白球,搅匀后从中摸一个球,并放回搅匀再摸出第二个球,两次摸球只可能出现3种的结果.
13．直角三角形两直角边的长为5和12,则斜边上的中线的长是( )
A．6.5 B．13 C．5 D．12
三、解答题（第14、15题每题3分,第16题5分, 第17题10分,共21分）
14.计算
15.计算
16.一次函数的图象过点(2, 3), (3, 2),求一次函数的解析式.
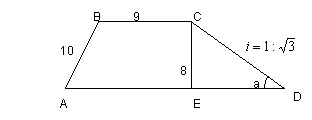
17.如图,一段河坝的横断面是梯形ABCD,试根据图中数据,求出坡角a和坝底宽AD.
B卷(50分)
一、填空题(每空2分，共10分)
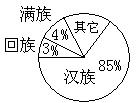
1、某地区约有80万人口，其中各民族所占比例如图所示，
则该地区少数民族人口共有约________万.
2.在Rt
ABC中，∠C=90°，AB=8，sinA=
，则AC= .
3.已知一个样本标准差S=
,则样本的平均数为
,样本容量为
.
4.计算：
+
-tan60°-
=________.
二、选择题(每小题3分,共9分)
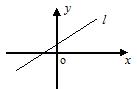5. 如图，直线l是一次函数y=k x + b (k ≠
0)的图象，则k、b的取值范围是( )
(A) k > 0， b < 0 (B) k > 0，b > 0
(C) k < 0， b > 0 （D） k < 0，b < 0
6. 有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有“20”、“08”和“北京”的字块，如果婴儿能够排成“2008北京”或“北京2008”，则他们就给婴儿奖励.假设该婴儿能将字块横着正排，婴儿能得到奖励的可能性是( )
(A) 
(B) 
(C) 
(D)
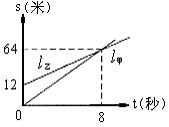7. 如图所示，l甲，l乙分别表示甲、乙两名学生运动情况的一次函数的图象，图中s和t分别表示运动路程和时间，根据图象判断快者的速度比慢者的速度每秒快（ ）
(A) 2.5米 (B) 2米 (C) 1.5米 (D) 1米
三、解答题（共31分.）
8.（9分）我们把三枚普通的硬币记作A、B、C，现抛掷这三枚硬币.
（1）(3分)画出树状图；
（2）(6分)根据树状图分析，出现三个正面、两正一反、两反一正的机会各是多少？
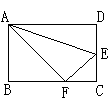9、(11分)矩形ABCD，折叠矩形的一边AD，使点D落在BC边的点F处，已知折痕AE=
cm,且tan∠EFC=。
(1) (6分)求证：△AFB∽△FEC；
(2) (5分)求矩形ABCD的周长。
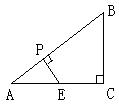10、(11分)如图，在△ABC中，∠C=90°，P为AB上一点，且点P不与点A重合，过点P作PE⊥AB交AC边上于E点，点E不与点C重合，若AB=10，AC=8，设AP的长为x，四边形PECB的周长为y，求y与x之间的函数关系式。
C卷(50分)
1.(4分)如图,在RtABC中,CD是斜边AB上的高,
已知AD=8,BD=2,则tanA+tanB= .
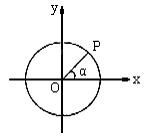2. (5分) 如图，以直角坐标系的原点O为圆心，以1为半径作圆，若P是该圆上第一象限内的一点，且OP与x轴正方向的夹角为α，则点P的坐标是(
)
(A) （cosα ,sinα） (B) (sinα, cosα)
(C) (1, cosα) (D) (1, sinα)
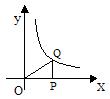3. (5分)如图，P是x轴正半轴上的一个动点，过点P作x轴的垂线PQ交双曲线
于点Q，连结OQ，当点P沿x轴向右运动时，Rt△QOP的面积( )
（A） 逐渐增大 （B）逐渐减少
（C） 保持不变 （D）无法确定
4．（12分）如图，某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B城市，经16小时的航行到达，到达后立即开始卸货．正在此时，接到气象部门通知，一台风中心正以40海里/时的速度由A向北偏西60°方向移动，距台风中心200海里的圆形区域（包括边界）均会受到影响．
问：B城市是否会受到台风的影响？若B城市会受到影响，该船应在多少小时内卸完货物（精确到0.1小时），以避免损失；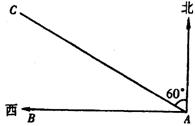
若B城市不会受到台风的影响，请说明理由．
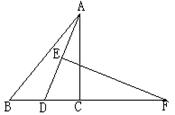5.（12分）在△ABC中，AD平分∠BAC，AD的垂直平分线交AD于E，交BC的延长线于F，试说明： 
(提示:连结FA,则
=
)
6、（12分）某计算器可以接受整数对转换，并且通过按一个键遵照如下的规则来改变数对，当原来的整数对（
）中的两个数之和
除以4分别余0，1，2，3时，输出的结果依次是（
），（
），（
），（
）．
（1）如果原来的整数对为（1，12），那么通过6次变换得到的整数对为（
），求
的值；
（2）如果原整数对按6次键后得到的整数对为（1，17），求原整数对的值．
八年级数学竞赛试卷参考答案
A卷
1. 
2.
6 3. 
4. （-2，-3） 5. （0，2） 6. 
7. 8cm 8. 6 9. 3 10. 2 CDA
14. 
15.
3 16. y=-x+5 17. 
B卷
1. 12 2. 
3. 100 20
4. 0 BCC 8. 1/8 3/8
3/8
9. (2)X=1 C=36cm 10. y=-3/2x+24
C卷
1. 2.5 2. A 3. C
4.答：B城市会受到台风的影响. …… （2分）
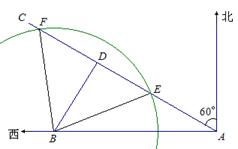画BD⊥AC于D, …… （1分）
由题意知，∠BAC=30°, AB=320 ,
所以BD=160…… （2分）
由于B城市到台风中心的运行路线
的距离为160海里，小于200海里，
所以B城市会受到台风的影响.（1分）
以B为圆心，200海里为半径画圆与AC交与E，F两点
由等腰三角形的性质和勾股定理知：DE=120, AD=
…… （3分）
所以，AE=－120≈157.13 ,
157.13÷40≈3.9 ,
所以该船应在3.9小时内卸完货物。…… （3分）
5．连接AF
因为EF垂直平分AD，所以FA=FD…… （1分）
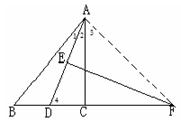所以∠4=∠2+∠3,即∠3=∠4－∠2……
（2分）
又因为∠4=∠1+∠B, ∠B =∠4－∠1…… （2分）
因为AD平分∠BAC，得∠1=∠2
所以∠3=∠B …… ……………… （2分）
再利用∠AFC =∠BFA ……………… （1分）
可得△AFC∽△ABF……………… （2分）
所以
，即
，
所以……………… （2分）
6、（1）从（1，12）
（1，13）（0，13）（0，14）（-1，14）
（-1，15）（-2，15），即
，所以
．（6分）
（2）逆推理，（1，17）
（1，16）（2， 16）（2，15）（3，15）
（3，14）（2，14）或（4，14），
即原整数对的值是（2，14）或（4，14）．（6分）