四边形单元试卷
班级_______姓名________座号_______评分______________
一 填空(每题3分,共30分)
1．平行四边形的周长为40，两邻边的比为2׃3，则这一组邻边长分别为________．
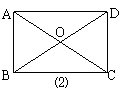
2、如图⑴已知O是□ABCD的对角线交点，AC＝24，BD＝38，AD＝14，那么△OBC的周长等于＿＿＿＿＿。
 | |||||||
 | |||||||
 | |||||||
 | |||||||
3、在平行四边形ABCD中，∠C＝∠B+∠D,则∠A＝＿＿＿，∠D＝＿＿＿。
4、一个平行四边形的周长为70cm，两边的差是10cm，则平行四边形较长边为＿＿＿＿cm。
5、已知菱形的一条对角线长为12cm，面积为30cm2，则这个菱形的另一条对角线长为__________cm。
6、菱形ABCD中，∠A＝60o，对角线BD长为7cm，则此菱形周长＿＿＿＿＿cm。
7、如果一个正方形的对角线长为
，那么它的面积＿＿＿＿＿＿。
8、如图2矩形ABCD的两条对角线相交于O,∠AOB＝60o,AB＝8,则矩形对角线的长＿＿＿。
9、如图3,等腰梯形ABCD中，AD∥BC，AB∥DE，BC＝8，AB＝6，AD＝5则△CDE周长＿＿＿。
10、如图4，BD是□ABCD的对角线，点E、F在BD上，要使四边形AECF是平行四边形，还需增加的一个条件是＿＿＿＿＿＿
二、选择题：（每小题3分，共30分）
11、在□ABCD中，∠A：∠B：∠C：∠D的值可以是（ ）
A、1︰2︰3︰4 B、1︰2︰2︰1 C、2︰2︰1︰1 D、2︰1︰2︰1
12、菱形和矩形一定都具有的性质是（ ）
A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线互相平分且相等
13、下列命题中的假命题是（ ）
A、等腰梯形在同一底边上的两个底角相等 B、对角线相等的四边形是等腰梯形
C、等腰梯形是轴对称图形 D、等腰梯形的对角线相等
14、四边形ABCD的对角线AC、BD交于点O，能判定它是正方形的是（ ）
A、AO＝OC，OB＝OD B、AO＝BO＝CO＝DO，AC⊥BD
C、AO＝OC，OB＝OD，AC⊥BD D、AO＝OC＝OB＝OD
15、给出下列四个命题
⑴一组对边平行的四边形是平行四边形
⑵一条对角线平分一个内角的平行四边形是菱形
⑶两条对角线互相垂直的矩形是正方形
⑷顺次连接等腰梯形四边中点所得四边形是等腰梯形。
其中正确命题的个数为（ ）
A、1个 B、2个 C、3个 D、4个
16、下列矩形中按虚线剪开后，能拼成平行四边形，又能拼成直角三角形的是（ ）
 |  |  |  | ||||||
| |||||||||
A B C D
17.如图，四边形ABCD是正方形，延长BC至点E，使CE=CA，连结AE交CD于点F，则∠AFC的度数是（ ）．
（A）150° （B）125° （C）135° （D）112．5°
18.如图，在等腰梯形ABCD中，AD∥BC，AC，BD相交于点O．有下列四个结论：①AC=BD；②梯形ABCD是轴对称图形；③∠ADB=∠DAC；④△AOD≌△ABO．其中正确的是（ ）．
（A）①③④ （B）①②④ （C）①②③ （D）②③④
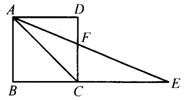
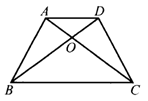
(17) (18)
19.给出四个特征(1)两条对角线相等;(2)任一组对角互补;(3)任一组邻角互补;(4)是轴对称图形但不是中心对称图形,其中属于矩形和等腰梯形共同具有的特征的共有 ( )
A.1个 B.2个 C.3个 D.4个
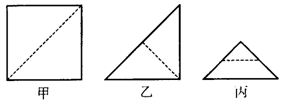
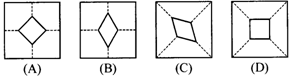
20.小许拿了一张正方形的纸片如图甲，沿虚线对折一次得图乙．再对折一次得图丙．然后用剪刀沿图丙中的虚线（虚线与底边平行）剪去一个角．打开后的形状是（ ）．
三.解答题(每题8分,共16分)
21.如图：在□ABCD中，∠BAD的平分线AE交DC于E，若∠DAE＝25o，
|
|
|
 | |||
| |||
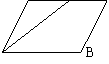
22.已知在梯形ABCD中，AD∥BC，AB＝DC，∠D＝120o,对角线CA平分∠BCD，且梯形的周长20，求AC。
 |
四.证明题(每题8分,共24分)
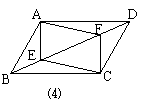
23.如图，△ABC中∠ACB＝90o，点D、E分别是AC，AB的中点，点F在BC的延长线上，且∠CDF＝∠A。
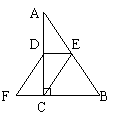求证：四边形DECF是平行四边形。
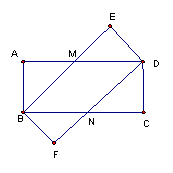
24. 如图四边形ABCD、DEBF都是矩形，AB＝BF，AD、BE交于M，BC、DF交于N。试说明四边形BMDN是菱形。
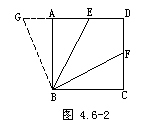
25. 如图，已知正方形ABCD中，E为AD上一点，BF平分∠EBC交DC于F，
求证：BE＝AE＋CF．
