19．1－19.2练习题
一、精心选一选(每小题2分，共20分)
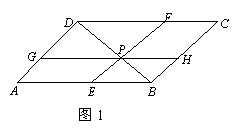1.如图1，在ABCD中，EF∥BC，GH∥AB,
EF、GH的交点P在BD上，图中面积相等
的平行四边形有（ ）对.
A.3 B.4 C.5 D.6
2.下列说法：①一组对边平行，另一组对边
相等的四边形是平行四边形；②一组对边平
行，一组对角相等的四边形是平行四边形；
③一组对边相等，一组对角相等的四边形是平行四边形.其中正确的有（ ）.
A.0个 B.1个 C.2个 D.3个
3.在四边形ABCD中，O是对角线的交点，能判定这个四边形为正方形的是（ ）.
A.AC=BD,AB∥CD，AB=CD B.AD∥BC，∠A=∠C
C.AO=BO=CO=DO D.AO=CO，BO=DO，AB=BC
4．能判定四边形ABCD是平行四边形的题设是（ ）.
A. AB∥CD, AD=BC B.∠A=∠B，∠C=∠D C.AB=CD，AD=BC D. AB=AD，CB=CD
5.在给定的条件中，能画出平行四边形的是（ ）.
A.以60cm为一条对角线，20cm、34cm为两邻边
B.以6cm、10cm为对角线，8cm为一边
C.以20cm、36cm为对角线，22cm为一边
D.以6cm为一条对角线，3cm、10cm为两邻边
6.正方形具有而菱形不一定具有的性质是（ ）.
A.对角线互相平分 B.对角线相等 C.对角线平分一组对角 D.对角线互相垂直
7.下列说法：①对角线互相垂直且相等的四边形是矩形；②对角线互相垂直平分的四边形是菱形；③对角线互相垂直的矩形是正方形；④对角线相等的菱形是正方形；⑤对角线互相垂直且相等的平行四边形是正方形；⑥对角线互相垂直且相等的四边形是正方形.其中错误的有（ ）.
A.1个 B.2个 C.3个 D.4个
8.如果平行四边形四个内角的平分线能围成一个四边形，那
么这个四边形是（ ）.
A.矩形 B.正方形 C.菱形 D.等腰梯形
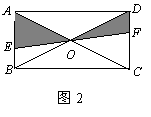
9.如图2，EF过矩形ABCD对角线的交点O，且分别交AB、CD
于E、F，那么阴影部分的面积是矩形ABCD的面积（ ）.
A.
B.
C.
D.
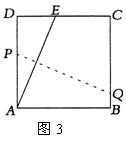
10.如图3，将一块边长为12的正方形纸片ABCD的顶点A折叠
至DC边上的点E，使DE=5，折痕为PQ，则PQ的
长为（ ）
A.12 B.13 C.14 D.15
二、耐心填一填（每小题3分，共30分）
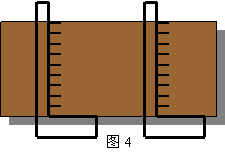
11.如图4所示，木板两边是线段，把两把曲尺的一边
紧靠木板边缘，再看木板另一边上刻度是否相等，就可
以判断木板的两个边缘是否平行，其根据是_______
_______________________________________________.
12.已知线段BC和BC外一点A，则以A为顶点，以线
段BC为一边的平行四边形有____个；以A为顶点，以线段BC为对角线的平行四边形有____个；以A、B、C为顶点的平行四边形有___个.
13.工人师傅在做门窗或矩形零件时，不仅要测量两组对边的长度是否分别相等，常常还要测量它们的两条对角线是否相等，以确保图形是矩形，这样做的道理是_______________
_________________________________________________________________________.
14.已知菱形ABCD的边长是2cm，∠BAD＝120°，则其对角线的长分别为____________，面积为_________.
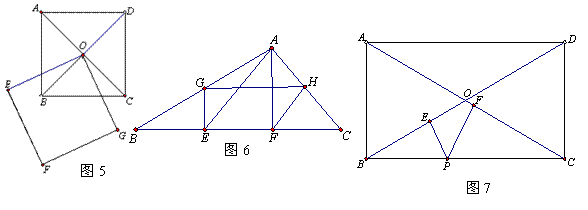
15.如图5，正方形ABCD的对角线相交于点O，点O是正方形EFGO的一个顶点，已知这两个正方形的边长均为4，则当正方形EFGO绕点O转动时，两个正方形重叠部分的面积为_______.
16.如图6，在△ABC中，BC=5，EF为BC的三等分点，AE=13，AF=12，G、H分别为AB、AC的中点，则四边形EFGH的周长为_________，面积为__________.
17.已知，在四边形ABCD中，E、F、G、H分别为AB、BC、CD、DA的中点，①四边形EFGH为______四边形；②当四边形ABCD的对角线AC、BD满足条件____________时，四边形EFGH为矩形；③当四边形ABCD的对角线AC、BD满足条件____________时，四边形EFGH为菱形；④若四边形EFGH为正方形，则四边形ABCD必须满足的条件是________________.
18.已知ABCD的周长为60cm，对角线AC、BD相交于点O，△AOB的周长比△BOC的周长大8cm，则这个平行四边形的各边的长分别为________________________.
19.如图7，在矩形ABCD中，对角线AC、BD相交于点O，点P为BC边上任意一点，PE⊥BD于E，PF⊥AC于F，已知AB=3，BC=4，则PE+PF=_________.
20.我们通常把不完全重合的两个图形叫做不同的图形.如果用两个全等的锐角三角形采取不同的方法拼成四边形，可以拼成几个不同的四边形？可以拼成几个不同的平行四边形？将得到的结果填入下表中：
| 三角形的类型 | 可以拼成不同的四边形的个数 | 可以拼成不同的平行四边形的个数 |
| 两个全等的不等边三角形 | ||
| 两个全等的等腰三角形（底和腰不等） | ||
| 两个全等的等边三角形 |
三、细心做一做（共70分）
21.（6分）阅读下列内容并回答问题：
矩形、菱形、正方形都是平行四边形，但它们都是有特殊条件的平行四边形，正方形不仅是特殊的平行四边形，而且是邻边相等的特殊矩形，也是有一个角是直角的特殊；菱形.因此，我们可以利用矩形、菱形的性质来研究正方形的有关问题.
回答下列问题：
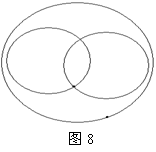
（1）将平行四边形、矩形、菱形、正方形填入它们的关
系图（图8）中；
（2）要证明一个四边形是正方形，可以先证明它是矩形，
再证明这个矩形的________________相等，或者先证明它
是菱形，再证明这个菱形有一个角是__________.
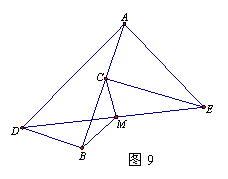22.（6分）如图9，△ABD和△ACE都是直角三角形，∠ABD=∠ACE=90°，M为DE的中点，CM⊥DE于M交AB于C.求证：MB=MC.
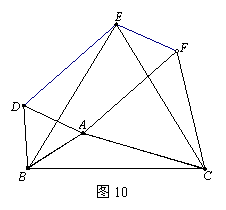
23.（8分）已知，如图10，以△ABC的三边为边在BC的同侧分别作三个等边三角形，即△ABD、△BCE、△ACF.请回答下列问题：
（1）四边形ADEF是什么四边形？
（2）当△ABC满足什么条件时，四边形ADEF是矩形？（不要求证明）
（3）当△ABC满足什么条件时，以A、D、E、F为顶点的四边形不存在？（不要求证明）
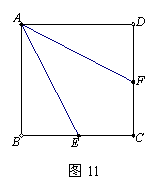24.（8分）已知，E是正方形ABCD的边BC的中点，F是CD上一点，AE平分∠BAF.
求证：AF=BC+CF.
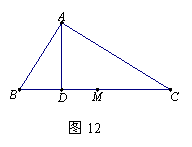
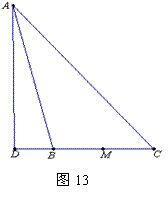
25.（10分）如图12，在△ABC中，∠B=2∠C，AD⊥BC于D，M为BC的中点.
（1）求证：DM=
AB；
（2）若点D不在线段BC上（在BC或CB的延长线上,如图13），则（1）中的结论还成立吗？请证明你的结论.
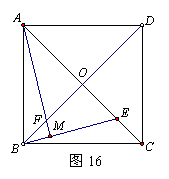
26.（10分）已知任意四边形ABCD，且线段AB、BC、CD、DA、AC、BD的中点分别是E、F、G、H、P、Q．
（1）若四边形ABCD如图14，判断下列结论是否正确（正确的在括号里填“√”，错误的在括号里填“×”）．
甲：顺次连接EF、FG、GH、HE一定得到平行四边形；（ ）
乙：顺次连接EQ、QG、GP、PE一定得到平行四边形．（ ）
（2）请选择甲、乙中的一个，证明你对它的判断．
（3）若四边形ABCD如图15，请你判断（1）中的两个结论是否成立？
27.（10分）如图l6，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，连结EB，过点A作AM
BE，垂足为M，AM交BD于点F．
(1)求证：OE=OF；
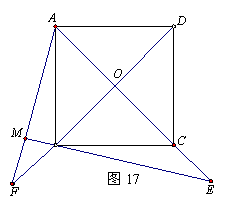(2)如图17，若点E在AC的延长线上，AMBE于点M，交DB的延长线于点F，其它条件不变，则结论“OE=OF”还成立吗?如果成立，请给出证明；如果不成立，请说明理由．
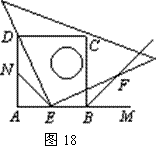
28．（12分）如图18、19，四边形ABCD是正方形，M是AB延长线上一点.直角三角尺的一条直角边经过点D，且直角顶点E在AB边上滑动（点E不与点A、B重合），另一条直角边与∠CBM的平分线BF相交于点F.
⑴如图18，当点E在AB边的中点位置时：
①通过测量DE，EF的长度，猜想DE与EF满足的数量关系是 ；
②连接点E与AD边的中点N，猜想NE与BF满足的数量关系是 _____；
③请证明你的上述两个猜想.
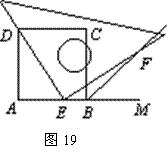
⑵如图19，当点E在AB边上的任意位置时，请你在AD边上找到一点N，使得NE=BF，进而猜想此时DE与EF有怎样的数量关系.
