八年级数学期末练习（一）
（满分100分，答卷时间100分钟） 命题人：高建宗
一、细心填一填：（每空2分，共38分）
1、如果△ABC沿北偏东45°的方向平行移动了2㎝，那么△ABC的一条高AD上的中点P向 方向移动了 ㎝.
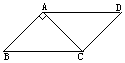
2、如图1，△ADE是由△ABC旋转得到的，AC=4，BC=3，则旋转中心是 ，DE= .
3、在□ABCD中，∠ABC的平分线分线段CD所成的两线段的长为4㎝、5㎝，则□ABCD的周长为
.
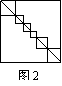
4、如图2，正方形ABCD的边长为8cm，把对角线分成几段，以每一段对角线作正方形，设这几个小正方形的周长和为
，则=_______.
5、如果等腰梯形两底之差等于一腰长，那么这个等腰梯形的锐角等于 _______.度.
6、菱形ABCD的周长为9.6㎝，且较大内角是较小内角的2倍，则菱形较短的对角线长为 ㎝.
翰林汇7、如图3,已知平行四边形ABCD中,AB=AC,AB⊥AC,A到BC的距离为1厘米.那么平行四边形ABCD的周长
8、如果直角梯形的上底为5㎝，高为4㎝，下底与一腰的夹角为45°，那么该梯形的面积为 ㎝2.
9、请你写出一个“矩形具有而平行四边形不具有”的特征 .
10、矩形的两条对角线相交所成的钝角为1200，矩形较短边的长为3.6
，则对角线的长为________。
11、如图4，等边三角形ABC中，D、E、F分别为三边BC、CA、AB中点，看一看数一数，其中三角形、菱形、等腰梯形共有 个 .
| 梯形个数 | 1 | 2 | 3 | 4 | 5 | … |
| 图形周长 | 5 | 8 | 14 | … |
12、观察下列图形（图5）和所给表格中的数据后回答问题：
（1）添满表格中所缺数据；
（2）当梯形个数为n时，这时图形的周为 .
 |
13、如图6，梯形ABCD中，AD∥BC，设AC与BD交于点O，则图中面积相等的三角形共有 对.
14、把直角三角形绕斜边的中点旋转 度后与原图形组成长方形.
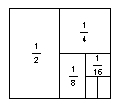
15、如图所示，把一个面积为1的正方形等分成两个面积为
的矩形，接着把面积为的矩形等分成两个面积为
的矩形，再把面积为的矩形等分为两个面积为
的矩形，如此进行下去，试利用图形揭示规律计算：
=_____。
二、精心选一选：（每题3分，共18分）
15、经过两次翻折(对称轴平行)后的图形,可以看成是原图形经过一次( )变换得到的
A、平移 B、旋转 C、旋转或平移 D、以上都不对
16、关于四边形ABCD：①两组对边分别相等；②两组对边分别平行；③有一组对边平行且相等；④对角线AC和BD相等；以上四个条件中可以判定四边形ABCD是平行四边形的有（ ）
A、1个 B、2 个 C、3个 D、4个
17、正方形是轴对称图形，它的对称轴共有（ ）
A、2条 B、3条 C、4条 D、6条
18、将一张菱形的纸片折一次，使得折痕平分这个菱形的面积，则这样的折纸方法共有（ ）
A、1种 B、2种 C、4种 D、无数种
19、下列说法不正确的是（ ）
A.对角线互相垂直平分的四边形是菱形 ;
B．对角线相等且互相平分的四边形是矩形
C．对角线互相垂直且相等的四边形是正方形;
D．一条对角线平分一组对角的平行四边形是菱形.
20、在四边形内找一点，使该点到各边距离都相等的图形是（ ）
A、平行四边形、矩形、菱形 B、菱形、矩形、正方形
C、矩形、正方形 D、菱形、正方形
三、用心想一想：
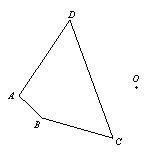
22、如图，作出四边形ABCD关于点O的中心对称图形。（6分）
 |
23、如图，点P是□ABCD的对角线BD上任意一点，过P作EF∥BC，分别交AB、CD于E、F，过P作HG∥AB，分别交AD、BC于G、H，请问四边形AEPG和PHCF的面积相等吗？并说明理由.（9分）
24、
如图，矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F，试说明四边形AFCE是菱形. （9分）
25、如图，△ACD、△AEB都是等腰直角三角形，∠CAD=∠EAB=90°，∠BAC=50°.
（1）若以A为旋转中心，请问逆时针旋转多少度，可使点D落在AB上.
（2）若连结EC、BD，请你猜想EC与BD关系？并用旋转的知识说明理由.
（10分）
．
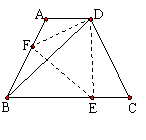
26. 如图，等腰梯形ABCD中，AD∥BC，∠DBC=45°.翻折梯形ABCD，使点B重合于点D，折痕分别交边AB、BC于点F、E. 若AD=2，BC=8.
求梯形ABCD的面积. （10分）
 |