数据的收集测试题
一、填空题
1、为了了解安徽电视台《第1时间》节目的收视率，宜采用的调查方式是 .
2、某市3万名初中结业生参加中考，为了考查他们的外语考试情况，命题组人员抽取500名考生的外语成绩进行统计分析，这个问题中的样本是 .
3、已知样本：7 10 8 14 9 7 12 11 10 8 13 10 8 11 10 9 12 9 13 11，那么样本数据落在范围8.5～11.5内的频率是
4、将一批数据分成5组，列出频率分布表，其中第一组与第五组的频率之和是0.27，第二与第四组的频率之和是0.54，那么第三组的频率是 .
5、在30个数据中，最小值是31，最大值为98，若取组距为8，可将这些数据分成 组.
6、甲、乙两同学在几次测验中，甲、乙平均分数都为86分，甲的方差为0.61，乙的方差为0.72，请你根据以上数据对甲、乙两同学的成绩作出评价： .
7、数据98，100，101，102，99的样本标准差是 .
8、已知x1，x2，x3的标准差是2，则数据x1+3，x2+3，x3+3的方差是
二、选择题
1、在统计中，样本的方差可以近似地反映总体的( )
A.平均状态 B.波动大小 C.分布规律 D.最大值和最小值
2、为了判断甲、乙两个小组学生英语口语测验成绩哪一组比较整齐，通常需要知道两组成绩的（ ）
A.平均数 B.方差 C.众数 D.频率分布
3、为了了解某校初三年级400名学生的体重情况, 从中抽查了50名学生的体重进行统计分析, 在这个问题中, 总体是指( )
A. 400名学生 B. 被抽取的50名学生
C. 400名学生的体重 D. 被抽取的50名学生的体重
4、有甲、乙两种水稻，测得每种水稻各10穴的分孽数后，计算出样本方差分别为
＝11，
=3.4，由此可以估计（ ）
A.甲比乙种水稻分蘖整齐 B.乙种水稻分蘖比甲种水稻整齐
C.分蘖整齐程度相同 D.甲、乙两种水稻分孽整齐程度不能比
5、一个样本有10个数据，各数据与样本平均数的差依次是-4，5，-2，4，-1，3，2，0，-2，-5，那么这个样本的方差是( )
A. 0 B. 104 C. 10.4 D. 3.2
6、某校初中三年级共有学生400人，为了解这些学生的视力情况，抽查了20名学生的视力，对所得数据进行整理.在得到的频数分布表中，若数据在0.95～1.15这一小组频率为0.3，则可估计该校初中三年级学生视力在0.95～1.15范围内的人数约为（ ）
A.6人 B.30人 C.60人 D.120人
7、在学校对学生进行的晨检体温测量中，学生甲连续10天的体温与36℃的上下波动数据为0.2，0.3，0.1，0.1，0，0.2，0.1，0.1，0, 0.1，则在这10天中该学生的体温波动数据中不正确的是（ ）
A.平均数为0.12 B.众数为0.1 C.中位数为0.1 D. 方差为0.02
8、将一组数据中每个数据的值都减去同一个常数，那么下列结论成立的是( ) A.平均数不变 B.方差和标准差都不变
C.方差改变 D.方差不变但标准差改变
9、人数相同的八年级(1)、(2)两班学生在同一次数学单元测试，班级平均分和方差如下：
，
，
，则成绩较为稳定的班级是（ ）
A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定
10、在方差计算公式
中，数字10和20分别表示（ ）
A.数据的个数和方差 B.平均数和数据的个数
C.数据的个数和平均数 D.数据组的方差和平均数
三、解答题
1．某农户承包荒山种了44棵苹果树.现在进入第三年收获期.收获时，先随意摘了5棵树上的苹果，称得每棵树摘得的苹果重量如下(单位：千克)
35 35 34 39 37
(1)在这个问题中，总体指的是 ，个体指的是 ，样本是 。
(2)试根据样本平均数去估计总体情况，你认为该农户可收获苹果大约多少千克？
(3)若市场上苹果售价为每千克5元，则该农户的苹果收入将达到多少元？
2．为了从甲、乙两名同学中选拔一个射击比赛，对他们的射击水平进行了测验，两个在相同条件下各射击10次，命中的环数如下(单位：环)
甲：7 8 6 8 6 5 9 10 7 4
乙：9 5 7 8 6 8 7 6 7 7
(1)求
，
，
，
；
(2)你认为该选拔哪名同学参加射击比赛？为什么？
3．为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况，从中抽取了部分学生的成绩(得分取整数，满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题(将答案直接填在横线上)：
| 分组 | 频数 | 频率 |
| 50.5～60.5 | 4 | 0.08 |
| 60.5～70.5 | 0.16 | |
| 70.5～80.5 | 10 | |
| 80.5～90.5 | 16 | 0.32 |
| 90.5～100.5 | ||
| 合计 | 50 | 1.00 |
(1)填充频率分布表的空格；
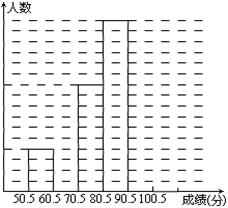(2)补全频数直方图，并绘制频数分布折线图；
(3)在该问题中，总体、个体、样本和样本容量各是什么？
(4)全体参赛学生中，竞赛成绩落在哪组范围内的人数最多？
(5)若成绩在90分以上(不含90分)为优秀，则该校成绩优秀的约为多少人？