淮南十三中2005——2006年度第一学期
八年级数学竞赛试题 得分
一、选择题：（5×5=25）
1、已知x、y都是质数，则方程x+y=1999共有（ ）
A 、1组解 B、2组解 C、3组解 D、4组解
2、已知一次函数y=（a—2）x+1的图象不经过第三象限，化简
+
的结果是（ ）
A、 5—2a B、 2a—5 C、 —1 D、 1
 |  | ||
|
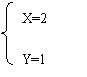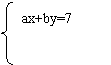A、4a+c=9 B、2a+c=9 C、4a-c=9 D、2a-c=9
4、甲是乙现在的年龄时，乙10岁；乙是甲现在的年龄时，甲25岁，那么（ ）
A、甲比乙大5岁； B、甲比乙大10岁；
C、乙比甲大10岁； D、乙比甲大5岁；
5、自然数x、y满足
+
=7，则x+y的值是（ ）
A、5 B、6 C、7 D、8
二、填空题（5×5=25）
1、 在直角坐标系xOy中，x轴上的动点M（x，0）到定点P（5，5）、Q（2，1）的距离分别为MP和MQ。当MP+MQ取最小值时，点M的坐标是______________。
2、
若a，b满足3
+5∣b∣=7，则S=2—3∣b∣的取值范围是____________。
mx+2y=10
3、m为正整数，已知二元一次方程组 有整数解，即x、y均为整数，
3x-2y=0
则m
_________________。
—
=
4、方程组 的解是_____________.
2x+y+
=6
5、已知
—︱b│=3，那么代数式+︱b│的值是___________
三、解答题（共七题，你可以在这七中任意选五题，每题10分，共50分）
1、 试说明：不论k为何值，一次函数（2k—1）x—（k+3）y—（k—11）=0的图象恒过一定点，并求出这个定点。
2、
知：如图，矩形QMNP的一边QM在边长为2的正三角形ABC的一边BC上，点P、N分别在AB、AC上，设MN=x，S
=y。
（1） 写出x的取值范围；
（2）
用x表示y；
A
（3）
当y取得最大值时，求证：S
=S
+S
P
N
B Q M C
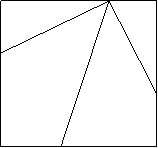
3、 如图，EFGH是正方形ABCD的内接四边形，∠BEG与∠CFH都是锐角，已知EG=3 ，FH=4，四边形EFGH的面积是5，求正方形ABCD的面积。
A H D
E
G
B F C
4、
坐标系中有三点A（0，1），B（1，3），C（2，6），已知直线y=ax+b上横坐0、1、2的点分别为D，E，F。
试求a，b的值使得AD+BE+CF达到的最小值。
=1
5、 求解方程组 （b≠2c，c≠—2b）
=2
6、已知：如图，A、B分别是x轴上位于原点左、右两侧的点，点P（2，p）在第一象限，直线PA交y轴于点C（0，2），直线PB交y轴于点D，S
=6
（1）⊿COP的面积
y
（2）求点A的坐标及p的值
D
（3）若S
=S
，求直线BD的函数解析式
P
x
A O B
7、如图，一机器人在点A处发现一个小球自点B处沿x轴向原点O方向匀速滚来，机器人立即从A处匀速直线前进，去截小球。若小求滚动速度与机器人行走速度相等，试在图中标出机器人最快能截住小球的位置C（尺规作图），并试分析原因。
y
A
O
B x