周巷镇八年级（下）数学竞赛试题
（考试时间 120分钟 满分 120分 可使用函数型计算器）
一、选择题（每小题4分，共40分）
1、若
，则
一定是（ ）
A、正数 B、负数 C、非负数 D、非正数
2、某手表每小时比准确时间慢3分钟，若在清晨4点30分时与准确时间对准，则当天上午该手表指示时间是10点50分时，准确时间应该是（ ）
A、11点10分 B、11点9分 C、11点8分 D、11点7分
3、下列说法正确的个数有（ ）
①等边三角形有三条对称轴；②在
中，若
，则不是直角三角形；③等腰三角形的一边长为4，另一边长9，则它的周长为17或22；④一个三角形中至少有两个锐角
A、1个 B、2个 C、3个 D、4个
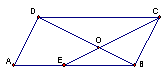
4、如图所示，在平行四边形ABCD中，CE是
的平分线，且交AB于E，DB与CE相交于O，已知AB=6，BC=4，则
等于（
）
A、
B、
C、
D、不一定
5、已知一组数据6，8，10，x的中位数与平均数相等，这样的x有( )
A、 1个 B、 2个 C、 3个 D、 4个以上（含4个）
6、若
（
是实数），则M的值一定是（ ）
A、正数 B、负数 C、零 D、整数
7、由方程
确定的曲线所围成的图形的面积是（
）
A、1
B、2
C、
D、4
8、在同一直角坐标系中，解析式为
的直线有无数条，在这些直线中不论怎样抽取，问至少要取多少条直线才能保证其中有两条直线经过完全相同的象限（
）
A、4条 B、5条 C、6条 D、7条
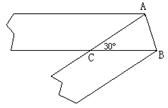
9、如图所示,将宽为4厘米的纸条折叠,折痕为AB，如果
∠ACB=30°,折叠后重叠部分的面积为（ ）平方厘米
A、16 B、14 C、12 D、4
10、对于每个
，函数
是
这三个函数中的最小值，则函数的最大值是（
）
A、4 B、6 C、8 D、
二、填空题（每小题4分，共40分）
11、化简：
12、给你0、1、2、3，最多可组成 个四位数
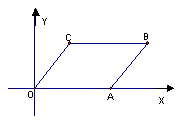
13、如图所示，在直角坐标系中，平行四边形OABC的顶点坐标B（17，6），C（5，6），直线
恰好将平行四边形OABC的面积分成相等的两部分，那么
=
14、已知一个梯形的四条边长分别为1，2，3，4，则此梯形面积等于
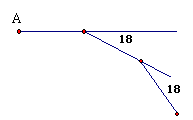
15、如图所示，某人从A点出发，每前进10m，就向右转
18°………这样下去，他第一次回到出发地A时，一共走
了 m
16、已知四个正数
、、
、
满足＜＜＜，它们两两的和按照从小到大的次序分别是：23、26、29、33、、，则
的值为
．
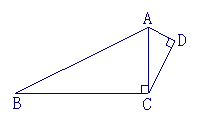17、如图，在两个直角三角形中，∠ACB=∠ADC=
，AC=
，AD=2，那么当AB的长等于__
___时，使得两个三角形相似．
18、已知一次函数
的图像经过点P（1，2），且与x轴正半轴交于点A，与y轴正半轴交于点B，若
，则点B的坐标为
19、已知
，且
，（其中
是锐角），则
=
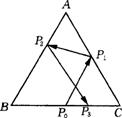20、如图，已知边长为2的正三角形ABC中，P0是BC边的中点，一束光线自P0发出射到AC上的点P 1后，依次反射到AB、BC上的点P 2和P3(反射角等于入射角)，若BP3=
，
则P1C长为
三、解答题（每小题10分，共40分）
21、一罐咖啡甲乙两人一起喝10天喝完，甲单独喝则需12天喝完；一斤茶叶用来泡茶甲乙两人一起喝12天喝完，乙单独喝则需20天喝完。假设甲有茶叶的情况下绝不喝咖啡，而乙有咖啡的情况下绝不喝茶。则甲乙两人一起用完一斤茶叶和一罐咖啡需多少天？
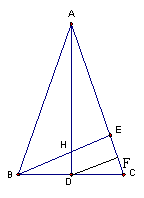
22、如图，中，AB=AC，高AD、BE相交于点H，AH=8，DH=1
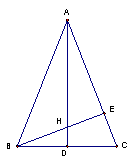求：（1）
的值
（2）
的值
23、预计用1500元购买甲商品个，乙商品个，不料甲商品每个涨价1.5元，乙商品每个涨价1元，尽管购买甲商品的个数比预定数减少10个，总金额仍多用29元．又若甲商品每个只涨价1元，并且购买甲商品的数量只比预定数少5个，那么甲、乙两商品支付的总金额是1563.5元．
（1）求、的关系式；
（2）若预计购买甲商品的个数的2倍与预计购买乙商品的个数的和大于205，但小于210，求、的值．
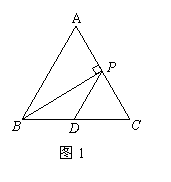
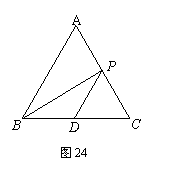24、如图24，正三角形ABC的边长为a，D是BC的中点，P是AC边上的点，连结PB和PD得到△PBD。求：
⑴当点P运动到AC的中点时，△PBD的周长；
⑵△PBD的周长的最小值。
周巷镇八年级（下）数学竞赛参考及评分标准
一、选择题：DBCBC ABDAB
二、填空题：11、
；12、192；13、
；14、
；15、200；16、75；
17、3或
；18、
；19、1；20、
三、解答题
21、解：设乙单独喝咖啡需要a天，则
——（2分）
解得：
——（3分）
设甲单独喝茶需要b天，则
——（5分）
解得：b=30——（6分）
现在甲先喝茶30天，一人把一斤茶叶喝完，同时乙喝了30天咖啡，然后两人再一同喝咖啡x天，则
——（8分）
解得x=5——（9分）
答：甲乙两人一起用完一斤茶叶和一罐咖啡需35天——（10分）
22、解：（1）过D作DF∥BE交AC于F——（1分）
则
——（2分）
又
——（4分）
所以，
所以，
——（6分）
（2）易知
∽
——（7分）
与联合解得：
——（8分）
又HD=1 所以，
——（9分）
所以，
——（10分）
23．（1）设预计购买甲、乙商品的单价分别为元和元，则原计划是
， ①
由甲商品单价上涨1. 5元、乙商品单价上涨1元，并且甲商品减少10个的情形，得
．②
再由甲商品单价上涨1元，而数量比预计数少5个，乙商品单价上涨仍是1元的情形，得
， ③
由①、②、③得
|
④－⑤×2并化简，得
．
（2）依题意，有205＜
＜210及，54＜＜
，
由是整数，得
，从而得
．
答：（1）、的关系；
（2）预计购买甲商品76个，乙商品55个．
24、⑴如图1，当点P运动到AC的中点时，BP⊥AC，DP∥AB， （2分）
所以 
，
，
，
（4分）
即△ABC的周长为BP＋DP＋BD=
。
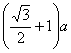（5分）
⑵如图2，作点B关于AC的对称点E，连结EP、EB、ED、EC，则PB＋PD=PE＋PD，因此ED的长就是PB＋PD的最小值，即当点P运动到ED与AC的交点G时，△PBD的周长最小。 （7分）
从点D作DF⊥BE，垂足为F，因为BC=a，所以，
。
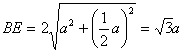因为∠DBF=30°，所以
，
，
，
。
（9分）
所以△PBD的周长的最小值是
。
（10分）