初二数学下学期期中综合训练题（无答案）

初二数学下学期期中复习综合训练

一、选择题：

1、若分式的值为零，则x的值是　　　　　　　　　　　　　　　　　　　 （　 ）

　 A. 1　　　　　　　  B.　－1　　　　　  C. 2　　　　　　　　　  D. 1或－1

2、关于x的分式方程有正数根, 则k的取值范围是　　　　　　　　　　 （　 ）

　 A. 　　　　　B. 　　　　　 C. 　　　　　D.

3、若正比例函数y = ax和反比例函数没有交点，则a与b的关系是　　　　　　  （　 ）

A. 同号　　　　　  B. 互为相反数　　　 C.异号　　　　　　　　 D. 互为倒数

4、若反比例函数的图象经过点A（x₁，－1）、B（x₂，2）、C（x₃，3）三点，则下列不等式成立的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）　　　　　　　　　　　　　　　　　　　　　　　　　　　　

A. x₁＜x₂＜x₃　　　　B. x₂＜x₁＜x₃　　　　 C. x₃＜x₂＜x₁　　　　　  D. x₁＜x₃＜x₂

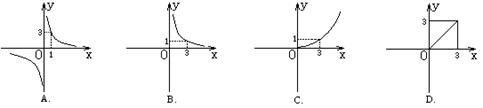
5、已知圆柱的侧面积是6π（cm²），若圆柱低面半径为x（cm），高为y（cm），则y关于x的函数图象大致是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　 ）

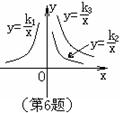6、如图，三个反比例函数在x轴上方的图象，

则k₁、k₂、k₃的大小关系是（　 ）

A. k₁＞k₂＞k₃　 B. k₃＞ k₂＞ k₁　 C. k₂＞k₃＞ k₁　 D. k₃＞k₁＞k₂

7、有一个三角形两条边长分别为4和5，要使三角形为直角三角形，

则第三边长为（　 ）

　 A. 3或　　B.　　　　  C. 或3　　D. 不确定

8、△ABC中，AB = 13，AC = 20，BC = 21，则△ABC的高AD为　　　　　　　　　 （　 ）

　　　 A. 不能确定　 B. 5　　　　　　 C. 12　　　　　 D. 16

二、填空题：

9、已知，则m =　　　 ；n =　　　 .

10、已知是方程的一个增根，则　　　.

11、若反比例函数的图象经过第二、四象限，则=　 .

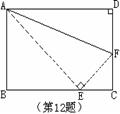
12、如图，在矩形ABCD中，AB = 8，AD =10，按如图所示折叠使点D

落在BC上的点E处，则EF的长为　　　 .

三、解答题：

13、已知，求的值.

14、解下列分式方程：

　 （1）；

（2）

15、已知，如图△ABC中，AB = AC，∠ABC = 45⁰，AD、BE分别为△ABC的高和中线，AD、BE相交于点H.

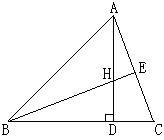（1）求证：BH = 2AE；

（2）若DH = 1，求AC²的值.

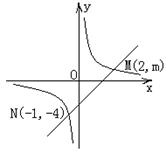
16、如图，一次函数的图象与反比例函数的图象交于M、N 两点.

　　　（1）求反比例函数和一次函数的解析式；

　　　（2）根据图象写出使反比例函数的值大于一次函数的值的取值范围.

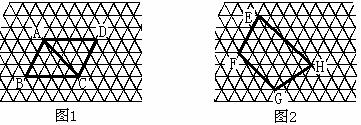
17、图中的虚线网格我们称之为正三角形网格，它的每一个小三角形都是边长为1个单位长度的正三角形，这样的三角形称为单位三角形。

（1）直接写出单位正三角形的高与面积；

（2）图1中的平行四边形ABCD含有多少个单位正三角形？ABCD的面积是多少？

（3）求出图1中线段AC的长（可作辅助线）；

（4）求出图2中四边形EFGH的面积.

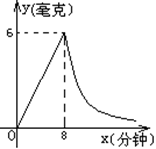
18、为了预防“非典”，某学校对教室采用药熏消毒法进行消毒. 已知药物燃烧时，室内每平方米空气中的含药量y（毫克）与时间x（分钟）成正比例，药物燃烧后，y与x成反比例（其图象如图所示）. 观察得药物8分钟燃毕. 此时室内空气中每立方米的含药量为6毫克，请根据题中所提供的信息，解答如下问题：

　　　　（1）药物燃烧时，y关于x的函数关系式为　　　　；自变量x的取值范围是　　　　；药物燃烧后，y关于x的函数关系式为　　　　  .

　　　　（2）研究表明，当空气中每立方米的含药量低于1.6毫克时学生方可进教室，那么从消毒开始，至少需要经过　　　　分钟后，学生才能回到教室？

　　　　（3）研究表明，当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟，才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？