八年级数学(下)第十九章平行四边形单元检测

八年级数学(下)第十九章平行四边形单元检测

(时间90分钟　满分100分)

班级　　　  学号　　　　  姓名　　　　　 得分　　　　 

一、选择题(每小题3分，共24分)

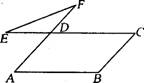1．在平行四边形ABCD中，∠B=110°，延长AD至F，

延长CD至E，连结EF，则∠E＋∠F＝(　　)

A．110° 　　　 B．30°　　C．50°　　　　　D．70°

2．菱形具有而矩形不具有的性质是  (　　)

A．对角相等　　 　 B．四边相等　　 C．对角线互相平分　  D．四角相等

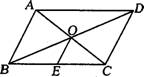3．如图，平行四边形ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=3 cm，则AB的长为　(　　)

A．3 cm 　　B．6 cm 　　C．9 cm 　　D．12 cm

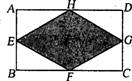4．已知：如图，在矩形ABCD中，E、F、G、H分别为边AB、BC、CD、DA的中点．若AB＝2，AD＝4，则图中阴影部分的面积为　　(　　)

A．8　　　　　B．6　 　　 C．4 　　　 D．3

5．用两块全等的含有30°角的三角板拼成形状不同的平行四边形，最多可以拼成　　(　  )

A．1个　　　　　 B．2个　　　　 C．3个　　　　 D．4个

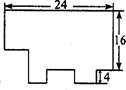6．如图是一块电脑主板的示意图，每一转角处都是直角，数据如图所示(单位：mm)，则该主板的周长是　　(　　)

A．88 mm　　　　　　　　　　　　　 B．96 mm

第6题

C．80 mm 　　　　　　　　　　D．84 mm

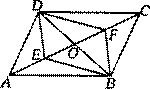7．如图，平行四边形ABCD中，对角线AC、BD相交于点O，E、F是AC上的两点，当E、F满足下列哪个条件时，四边形DEBF不一定是平行四边形　　(　　)

第7题

A．∠ADE＝∠CBF　　　 B．∠ABE＝∠CDF

C．OE＝OF　　　　　　D．DE＝BF

8．如图是用4个相同的小矩形与1个小正方形镶嵌而成的正方形图案．已知该图案的面积为49，小正方形的面积为4，若用x、y表示小矩形的两边长(x＞y)，请观察图案，指出以下关系式中不正确的是　　( 　 )

第8题

A．　　　　　　　 B．

C．　　　　　D．

二、填空题(每小题4分，共24分)

9．若四边形ABCD是平行四边形，请补充条件　　　　　

(写一个即可)，使四边形ABCD是菱形．

第10题

10．如图，在平行四边形ABCD中，已知对角线AC和BD相交于点O，△ABO的周长为15，AB＝6，那么对角线AC＋BD＝　　　　 

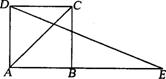11．如图，延长正方形ABCD的边AB到E，使BE＝AC，则∠E＝　　　°．

第11题

12．已知菱形ABCD的边长为6，∠A＝60°，如果点P是菱形内一点，且PB＝PD＝，那么AP的长为　　　　　　　 ．

13．在平面直角坐标系中，点A、B、C的坐标分别是A(－2，5)，B(－3，－1)，

C(1，－1)，在第一象限内找一点D，使四边形ABCD是平行四边形，那么

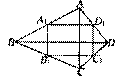点D的坐标是　 　　 ．

14．如图，四边形ABCD的两条对角线AC、BD互相垂直，

 A₁B₁C₁D₁是中点四边形．如果AC＝3，BD＝4，

第14题

那么A₁B₁C₁D₁的面积为　　　　　 

三、解答题(52分)

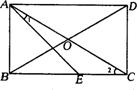
15．(8分)如图，在矩形ABCD中，AE平分∠BAD，∠1＝15°．

(1)求∠2的度数．(2)求证：BO＝BE．

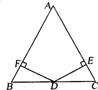
16．(8分)已知：如图，D是△ABC的边BC上的中点，DE⊥AC，DF⊥AB，垂足分别为E、F，且BF＝CE．当∠A满足什么条件时，四边形AFDE是正方形?请证明你的结论．

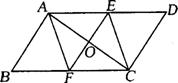
17．(8分)如图，在平行四边形ABCD中，O是对角线AC的中点，过点O作AC的垂线与边AD、BC分别交于E、F．　求证：四边形AFCE是菱形．

18．(8分)已知：如图，在正方形ABCD中，AC、BD交于点O，延长CB到点F，使　

BF＝BC，连结DF交AB于E．求证：OE＝(　　)BF(在括号中填人一个适当的常数，再证明)．

19．(8分)在一次数学探究活动中，小强用两条直线把平行四边形ABCD分割成四个部分，使含有一组对顶角的两个图形全等．

(1)根据小强的分割方法，你认为把平行四边形分割成满足以上全等关系的直线有

　　 组．

(2)请在下图的三个平行四边形中画出满足小强分割方法的直线．

(3)由上述实验操作过程，你发现所画的两条直线有什么规律?

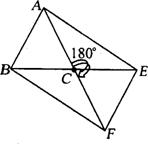
20．(12分)已知：如图，在△ABC中，AB＝AC，若将△ABC绕点C顺时针旋转180°得到△FEC．

　(1)试猜想线段AE与BF有何关系?说明理由．

　(2)若△ABC的面积为3 cm²，请求四边形ABFE的面积．

　(3)当∠ACB为多少度时，四边形ABFE为矩形?说明理由．