八年级（下）数学期末试卷
班级 号次 姓名
一、填空题：（每小题3分，共30分）
1、当x 时，式子
有意义.
2、在△ABC中，∠C=90o，E是AB边上的中点，CD⊥AB，且AB=2AC。若AC=3，则AB= ，CE= ，CD= .
3、如果y与x-2成反比例，且当x=3时，y=2；则当x=－3时，y= .
4、某函数图象经过点（－1，2），且函数y的值随x的增大而增大，请你写出一个符合条件的函数关系式： .
5、已知三角形三边满足：（a－40）2+（b－9）2+
=0，则这个三角形的形状是
.
6、在Rt△ABC中，AC＝6，BC＝8，则该三角形的斜边上的高为_______。
 |
7、甲、乙两人射击比赛，平均环数相同，其中甲的方差是5，
且乙的环数分别为：5，6，9，10，5，那么成绩
较为稳定的是 .
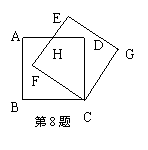
8、如图，边长为3的正方形ABCD绕点C按顺时针方向
旋转30o后，得到正方形EFGH，EF交AD于H，
那么DH= .
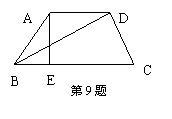
9、如图，在梯形ABCD中，AD∥BC，∠ABC=60o，
BD=2
，AE是梯形的高，且BE=1，则AD= .
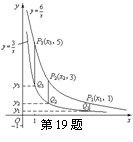10.两个反比例函数
，
在第一象限内的图象如图所示,
点P1，P2，P3，…，P2 005在反比例函数图象上，它们的横坐
标分别是x1，x2，x3，…，x2 005，纵坐标分别是1，3，5，…，共
2005个连续奇数，过点P1， P2，P3，…，P2 005分别作y轴的平行
线，与的图象交点依次是Q1（x1，y1），Q2（x2，y2），
Q3（x3，y3），…，Q2 005（x2 005，y2 005），则y2 005= ．
二、选择题：（每小题3分，共30分）
11、计算式子：
·÷·的结果是
（ ）
A.
1
B. 0 C. -1 D. 
12、某服装销售商在进行市场占有率的调查时，他最应该关注的是（ ）
A.服装型号的平均数 B.服装型号的众数 C.服装型号的中位数 D.最小的服装型号
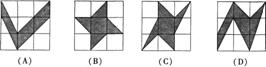13、在右面图形中，每个大正方形网格都是由边长为1的小正方形组成，则图中阴影部分面积最大的是( )
14、若关于
的方程
有增根，则
的值是（ ）
A．－2
B．2 C．5 D．3
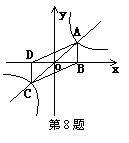
15、正比例函数y=x与反比例函数y=
的图象相交于A、C两点.
AB⊥x轴于B,CD⊥y轴于D(如图),则四边形ABCD的面积为( )
A.
1 B.
C.
2 D.
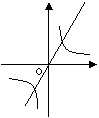
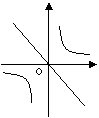
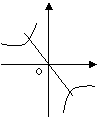
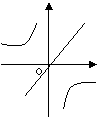16、已知a＜0，则函数y=ax和函数y=
图象大致是（ ）
A. B. C. D.
17、若一组数据分别为x
，x
，…… x
的平均数和方差分别为
和S
，则3x+2，3x+2，…… 3x+2的平均数和方差分别是（ ）.
A.
3+2和S
B. 3+2和3S+2
C. 3+2和3S D. 3+2和9S
18、 一平行四边形边长为10cm，一对角线为12cm，则另一对角线的长度x的取值范围是（ ）。
A. 2 ＜x＜22 B. 2 ＜x＜11 C. 4 ＜x＜16 D. 8 ＜x＜32
19.已知等腰梯形ABCD中，AD∥BC，AE∥DC，∠B=60º，BC=3，△ABE的周长为6，则等腰梯形的周长是 （ ）
A. 8 B . 10 C. 12 D. 16
20、反比例函数y=
的图象上两点A（x
，y
），B（x，y），当x＜0＜x时，有y
＜y，则m的取值范围为（ ）.
A.
m＜0 B. m＞0 C. m＜
D. m＞
三、简答题：（共七题，总分60分）
21、（6分）化简求值：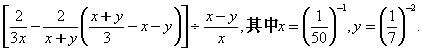
22、（8分）一定质量的氧气，它的密度ρ（kg/m3）它的体积V（m3）的反比例函数，当V=10 m3时，ρ=1.43 kg/m3。
（1）求ρ和V的函数关系式；
（2）求当V=2 m3时氧气的密度ρ.
 |
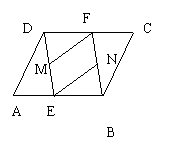23、（8分）如图，在 ABCD中，AE=CF，且M、N分别
是DE、BF的中点，求证：四边形ENFM是平行四边形.
24、（8分）已知：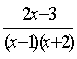
=
+
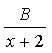，求A和B的值.
 |
25、（8分）在梯形ABCD中， AD∥BC，对角线AC⊥BD，
且AC=5cm，BD=12cm.求梯形的中位线.
26、（10分）市政府计划建设一项水利工程，工程需要运送的土石方总量为106m3，某运输公司承办了该项工程运输土石方的任务。
（1）运输公司平均每天工作量v（单位：米3/天）与完成运送任务所需的时间t（单位：天）之间具有怎样的函数关系？
（2）该公司共有100辆卡车，每天一共运送土石方104m3，则该公司完成这个任务需要多长时间？
（3）该公司以（2）中的速度工作了40天后，由于工程进度的需要，剩下的所有运输任务必须在50天内完成，公司至少需要再增加多少辆卡车才能按时完成任务？
27、（12分）顺次连结任意四边形ABCD的各边中点E、F、G、H，得到一个新的四边形：
（1）、试着猜一猜，这个四边形是什么四边形？并写出证明过程.
（2）、要使四边形EFGH成为一个矩形，需要增加什么条件？请你自己补充一个你认为正确的条件，并写出证明过程.
（3）、要使四边形EFGH成为一个菱形，又需要增加什么条件？请你自己补充一个你认为正确的条件，并写出证明过程.