2005学年八年级第二学期数学期末检测卷
(考试时间90分钟,满分120分)
一、 选择题(共15题,每题3分,共45分)
1.![]() 的平方根是 (
)
的平方根是 (
)
A.±4 B. +4 C. - 4 D. ±2
2.在![]() ,sin450,0,
,sin450,0,![]() ,0.…,
,0.…,![]() 这7个数中,无理数有( )
这7个数中,无理数有( )
A. 1个 B. 2个 C. 3个 D. 4个
3.能使![]() 有意义的x的范围是( )
有意义的x的范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.若某数的立方根等于这个数的算术平方根,则这个数等于( )
A. 0 B. ±2 C. –1或0 D. 1或0
5.在平面直角坐标系中,点P(4,-2)关于y轴的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.点A为正比例函数图象的一点,它到原点的距离为5,到x轴的距离为3,若点A在第二象限内,则这个正比例函数解析式为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 7.当
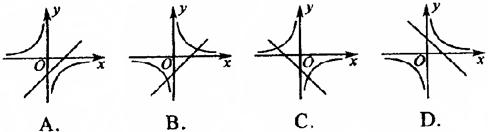
7.当![]() 时,函数
时,函数![]() 与
与![]() 在同一坐标系中的图象可能是( )
在同一坐标系中的图象可能是( )
8.![]() cos30°+
cos30°+![]() sin30°- tan60°·sin60°=( )
sin30°- tan60°·sin60°=( )
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
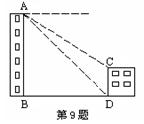
9.如图,两建筑物水平距离为32米,从点A测得
对点C的俯角为30o,对点D的俯角为45o,
则建筑物CD的高约为( ).
A.14米 B.17米 C.20米 D.22米
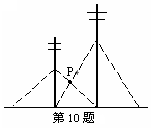 10.相邻两根电杆都用钢索在地面上固定,如图,一根电杆
10.相邻两根电杆都用钢索在地面上固定,如图,一根电杆
钢索系在离地面4米处,另一根电杆钢索系在离地面6米处,
则中间两根钢索相交处点P离地面( ).
A.2.4米 B.2.8米
C.3米 D.高度不能确定
11.△ABC和△A![]() B
B![]() C
C![]() 中,AB=9cm,BC=8cm,CA=5cm,A
中,AB=9cm,BC=8cm,CA=5cm,A![]() B
B![]() =3cm,B
=3cm,B![]() C
C![]() =
=![]() cm,C
cm,C![]() A
A![]() =
=![]() cm,那么( )
cm,那么( )
 A.∠A=∠A
A.∠A=∠A![]() B.∠A=∠B
B.∠A=∠B![]() C.∠A=∠C
C.∠A=∠C![]() D.∠C=∠B
D.∠C=∠B![]()
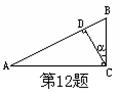
12.如图Rt△ABC中,∠ACB=90º,CD⊥AB于D,BC=3,
AC=4,设∠BCD=a,则tana的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13.野外生存训练中,第一小组从营地出发向北偏东60o方向前进了3千米,第二小组向南偏东30o方向前进了3千米,经观察、联系,第一小组准备向第二小组靠拢,则行走方向和距离分别为( ).
 A.南偏西15o,
A.南偏西15o,![]() 千米 B.北偏东15o,
千米 B.北偏东15o,![]() 千米
千米
C.南偏西15o,3千米 D. 南偏西45o,![]() 千米
千米
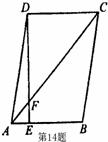
14.如图平行四边形ABCD中,![]() ,
,![]() ,
,
则![]() 的值是( )
的值是( )
A.12![]() B.24
B.24![]()
C.54![]() D.15
D.15![]()
15.已知一次函数y=![]() x+m和y=-
x+m和y=-![]() x+n的图像都经过点A(-2,0), 且与y轴分别交于B,C两点,那么△ABC的面积是 ( )
x+n的图像都经过点A(-2,0), 且与y轴分别交于B,C两点,那么△ABC的面积是 ( )
A. 2 B. 3 C. 4 D. 6
二、 填空题(共5题,每题4分,共20分)
16.已知![]() =
。
=
。
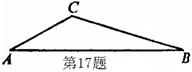 17.如图在
17.如图在![]() 中,
中,![]() ,
,
则![]() 的长为___________。
的长为___________。
18.关于x的一次函数y=ax+a+1的图像与y轴的交点在x轴上方,
且y随x的增大而减小,则a的取值范围是————————————。
19.若三角形的三边a、b、c满足a2-4a+4+![]() =0, 则笫三边c的取值
=0, 则笫三边c的取值
范围是_____________.
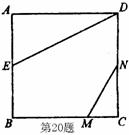 20.如图,正方形ABCD的边长为2,
20.如图,正方形ABCD的边长为2,![]() ,
,![]() ,
,
线段![]() 的两端在
的两端在![]() 、
、![]() 上滑动,当
上滑动,当![]() ________时,
________时,
![]() 与
与![]() 相似。
相似。
三、 解答题(共6题,共55分)
21.化简与计算(本题共10分,每题5分)
(1)3![]() -+
(2)
-+
(2)
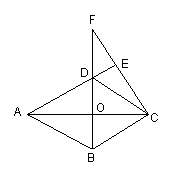
22.(本题共8分)
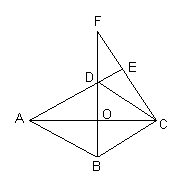
如图,菱形ABCD中,CF⊥AD,垂足为E,交BD的延长线于F.
求证:AO2=BO•OF.
23.(本题共8分)
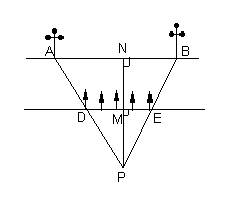
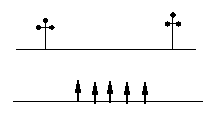 一条河的两岸有一段是平行的.在河的这一岸每相距5米在一棵树,在河的对岸每相距50米在一根电线杆.在这岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽.
一条河的两岸有一段是平行的.在河的这一岸每相距5米在一棵树,在河的对岸每相距50米在一根电线杆.在这岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽.
24.(本题共9分)
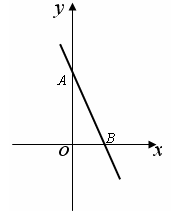 已知一条直线经过A(0,4)、点B(2,0),如图.将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D,使DB=DC.求直线CD的函数解析式.
已知一条直线经过A(0,4)、点B(2,0),如图.将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D,使DB=DC.求直线CD的函数解析式.
25.(本题共10分)
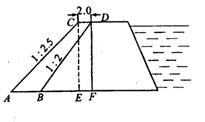 沿水库水坝的背水坡将坝面加宽2.0米坡度由原来的1:2改成1:2.5,已知原背水坡长BD=
沿水库水坝的背水坡将坝面加宽2.0米坡度由原来的1:2改成1:2.5,已知原背水坡长BD=![]() 米,坝长90米,求完成这一工程需多少方土(保留两个有效数字)。
米,坝长90米,求完成这一工程需多少方土(保留两个有效数字)。
26.(本题共10分)
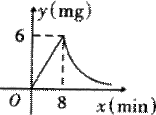 为了预防“非典”,某学校对教室采用药熏消毒法进行
为了预防“非典”,某学校对教室采用药熏消毒法进行
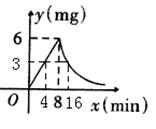
消毒,已知药物燃烧时,室内每立方米空气中的含药量
y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成
反比例(如图所示).现测得药物8min燃毕,此时室内
空气中每立方米的含药量为6mg,请根据题中所提供的
信息,解答下列问题:
(1)药物燃烧时,y关于x的函数关系式为_________,自变量x的取值范围是:___________;药物燃烧后,y关于x的函数关系式为:__________;
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过_________min后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
2005学年八年级第二学期数学期末检测答案卷
(考试时间90分钟,满分120分)
四、 选择题(共15题,每题3分,共45分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| D | D | D | D | C | B | A | B |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|
| A | A | B | A | A | C | C |
|
五、 填空题(共5题,每题4分,共20分)
![]()
![]()
![]() 16.
17.
18. -1 < a < 0
16.
17.
18. -1 < a < 0
![]() 19. 1 < C < 5 20.
19. 1 < C < 5 20.
六、 解答题(共6题,共55分)
21. 解下列方程(本题共10分,每题5分)
(1)3![]() -+
(2)
-+
(2)
解:=![]() 解:=
解:=![]()
 22. (本题共8分)
22. (本题共8分)
提示只要证ΔAOB∽ΔFOC,
其中要先说明∠BOA=∠F 或∠ABO=∠FCO,
再根据菱形得∠AOB=∠FOC=90O
 23. (本题共8分)
23. (本题共8分)
如图,由题知AB=50,DE=20,PM=25;
因DE∥AB,
∴ΔPDE∽ΔPAB,
从而PM∶PN=DE∶AB,
设MN=x米,则25∶(25+x)=20∶50,
x=37.5(米)
24. (本题共9分)
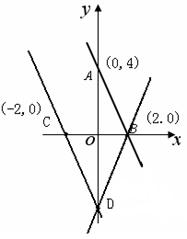
解:直线CD的函数解析式:
y=-2x-4
25.(本题共10分)
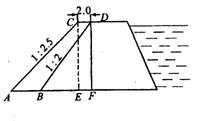 解:AB=5, CD=2 ,DF=6
解:AB=5, CD=2 ,DF=6
S=![]() (2+5)×6=21 (㎡)
(2+5)×6=21 (㎡)
V=21×90=1.9×103 (m3)
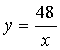
![]() 26.(本题共10分)
26.(本题共10分)
(1) 、 (0≤X≤8) 、 。
 (2)
30
。
(2)
30
。
(3)答:如图当空气中每立方米的含药量≥3mg,持续时间
为16-4=12 min时,能有效杀灭空气中的病菌,
因此这次消毒是有效的。