2006年6月四川省青神县八年级数学期末检测题
（120分钟完卷，满分120分）
一、选择题(每题3分，共36分)
1．
的平方根是( )
A．
B．9 C．±9 D．±3
2．点P(1，－2)关于原点对称的点的坐标是( )
A．(－2，－1) B．(－1，－2) C．(－1，2) D．(1，2)
3．在函数
中，自变量x的取值范围是( )
A．x≥0 B．x＜9 C．x＞0且x≠9 D．x≥0且x≠9
4．在下列根式中，与
是同类二次根式的是( )
A．
B．
C．
D．
5．如果点P(5，2＋a)在第四象限，则a的取值范围是( )
A．a＜－2 B．a≤－2 C．a＞－2 D．a≥－2
6．在△ABC中，∠C＝90°，如果tanA＝
，那么sinB的值等于( )
A．
B． C．
D．
7．数学老师对小华在期末的4 次数学模拟考试成绩进行统计分析，相知道小华的数学成绩是否稳定，则老师不想知道的是小华这4次数学成绩的( )
A．中位数 B．方差 C．标准差 D．极差
8．将直线y＝3x向上平移两个单位，所得直线是( )
A．y＝3x－2 B．y＝3x＋2 C．y＝3(x－2) D．y＝3(x＋2)
9．两位同学在描述同一反比例函数的图象时，甲同学说：这个反比例函数的图象与直线y＝－x有两个交点；乙同学说：这个反比例函数图象上一点到两坐标轴的距离的积都是5，你认为这两个同学所描述的反比例函数的解析式是( )
A．y＝－
B．y＝ C．y＝
D．y＝－
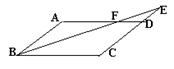
10．如图，四边形ABCD是平行四边形，则图中与△DEF相似的三角形共有( )
A．1个 B．2个 C．3个 D．4个
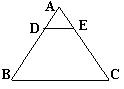
11．如图，在等边△ABC中，点D、E分别在AB、AC上，如果△ADE∽△ABC，AE∶AC＝1∶4，BC＝8cm，那么△ADE的周长等于( )
A．12cm B．6cm C．3cm D．2cm
12．如图所示是一束平行光线从教室外射入教室的平面示意图，测得光线与地面所成的角∠ABC＝30°，窗户的高在教室地面上的影长BD＝2
米，窗户的下檐到教室地面的距离EC＝1米，(点B、D、C在同一直线上)，则窗户的高AE为( )
A．1.5米 B．米 C．2米 D．3米
二、填空题(每题2分，共20分)
13．计算：
＝ ；
＝
。
14．在对
运算时，发现有＝6＋
＝6＋2＝8，请问是否还有其它这样的两位数也能用类似的方法来计算？请至少写出一个这样的两位数 。
15．在正比例函数y＝kx中，当x＝－2时，y＝6，则该函数的解析式是 。
16．两个相似三角形的面积比为9∶4，第一个三角形的周长为12cm，那么第二个三角形的周长为 。
17．△ABC中，∠C＝90°，其中两条边的长分别为10和6，
则第三边的长是 。
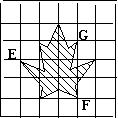
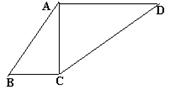
18．如图，若点E坐标为(－2，2)，点F坐标为 (1，0) ，则
点G的坐标为 。
19．某校举办“庆五四”歌咏比赛，六位评委给某班演出评分如下：89，92，95，96，93，则这组数据的极差是
。(单位：分)
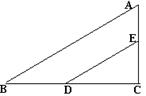
20．已知：如图，AC⊥BC，AD⊥AC，AD＞AC＞BC，请你添加一个条件使△ACD∽△CBA，你添加的条件是： 。
21．如果反比例函数y＝
(x＞0)的图象在第一象限，则
k ；写出一个图象在一、 二、 四象限的一次函数的
关系式 。
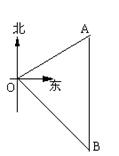
22．如图，位于O处的某海防哨所发现在它的北偏东60°方向相距600m的A地有一艘快艇正在向正南方向航行，经过若干时间快艇到达哨所东南方向的B处，则A、B间的距离是 米(结果保留根号)
三、解下列各题(每题5分，共15分)
23．
24．
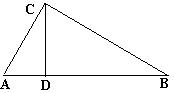25．如图，已知△ABC中，∠ACB＝90°，CD⊥AB于D，
若∠B＝30°，CD＝6，求AB的长(精确到0.1)
四、解下列各题(第26题7分，第27题8分，共15分)
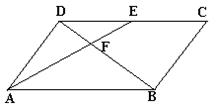
26．已知：如图，
ABCD中，E是CD的中点，
AE交BD于F
⑴找出图中的相似三角形，并说明理由
⑵若DF＝3，求BD的长
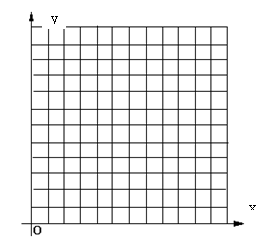
27．⑴在右图方格中指定的直角坐标系中，画出以A(2，4)、B(6，4)、C(6，7)为顶点的△ABC
⑵在同一平面直角坐标系画出△A’B’C’，且A’(1，2)、B’(3，2)、C’(3，3.5)，△A’B’C’与△ABC是否是相似三角形？
⑶思考：这两个三角形是位似三角形吗？如果是，写出位似中心的坐标；若不是，说明理由。
五、解下列各题(每题8分，共16分)
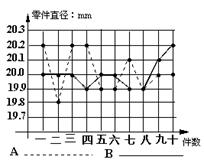28．为选派一名学生参加参加全市实践活动技能竞赛，A、B两位同学在学校实习基地进行加工直径为20mm零件的测试，他们各加工的10个零件的相关数据依次如下表所示(单位：mm) 根据测试得到的有关数据，试解答下列问题：
| 平均数 | 方差 | 完全符合要求的个数 | |
| A | 20 | 0.026 | 2 |
| B | 20 | SB2 | 5 |
⑴考虑平均数与完全符合要求的个数，你认为 的成绩好些。
⑵计算SB2的大小，考虑平均数与方差，说明谁的成绩好些。
⑶考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况，你认为派谁去参赛较合适？说明你的理由。
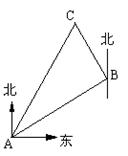29．在一次夏令营活动中，张川从营地A点出发，沿北偏东60°的方向走了500米到达B点，然后再沿北偏西30°方向走了500米到达目的地C点。
求：⑴A、C两地之间的距离
⑵确定目的地C在营地A的什么方向。
六、解下列各题(每题9分，共18分)
30．如图，Rt△OAB是一张放在平面直角坐标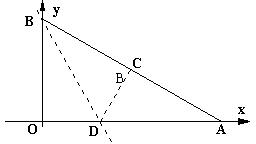
系中的直角三角形纸片，点O与原点重合。点A在x轴上，OB＝2，∠OAB＝30°，将Rt△OAB折叠，使OB边落在AB边上，点O与点C重合，折痕为BD。
⑴求折痕BD所在直线的解析式；
⑵求点C的坐标
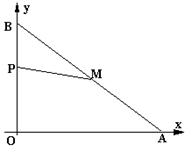31．如图，在平面直角坐标系内，已知点A(8，0)，点B(0，6)，动点P从点B开始在线段BO上以每秒1个单位长度的速度向点O移动，同时动点M从点A开始在线段AB上以每秒2个单位长度的速度向点B移动，设点P、M移动的时间为t秒。
⑴求Rt△OAB的面积；
⑵当t为何值时，△BPM与△BOA相似？
2006年6月四川省青神县八年级数学期末检测题参考答案
一、1~6．DCDDAC；7~12．ABABBC
二、13．－9，2；14．49，81；15．y＝－3x；16．8cm；17．8或2
；18．(1，3)；19．7；20．∠D＝∠BAC或∠ACD＝∠B或
；21．k＜0，y＝－3x＋1(不唯一)；22．(300＋300)cm
三、23．解：原式＝2＋18－4＋…4分＝20－3…5分
24．解：原式＝－1＋(
)2＋()2…3分＝－1＋
＋＝…5分
25．解：在△BDC中，BC＝
＝
＝12，…2分
在△ABC中，AB＝
＝
＝8≈13.1…5分
四、26．解：⑴△ABF∽△EDF …1分 ∵ABCD，∴AB∥CD…2分
∴∠ABF＝∠EDF，∠BAF＝∠DEF…3分 ∴△ABF∽△EDF…4分
⑵∵△ABF∽△EDF∴
…5分 ∵ABCD，E为CD中点
∴AB＝CD＝2DE…6分 ∴
＝2 ∴BF＝6…7分
27．解：⑴略；…3分 ⑵略，是；…5分 ⑶是位似形，位似中心是O…8分
五、28．⑴B …2分 ⑵∵SB2＝
[5(20－20)2＋3(19.9－20)2＋(20.1－20)2＋(20.2－20)2]
＝0.08…5分
且SA2＝0.026，∴SA2＞SB2 在平均数相同的情况下，B的波动小，∴B的成绩较好…6分
⑶从图中折线走势可知，尽管A的成绩前面起伏较大，但后来逐渐稳定，误差小，预测A有潜力，可选派A去参赛…8分
29．⑴AC＝1000米 …4分⑵∵tan∠BAC＝
…6分∴∠BAC＝30°…7分∴目的地在营地A的北偏东30°的方向…8分
六、30．⑴由题意知∠OBD＝∠DBC＝30°在Rt△OBD中，OD＝OB·tan30°＝2×
＝2，∴B(0，2)，D(2，0) …2分设所求解析式为y＝kx＋b，∴
∴
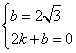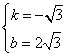…4分∴折痕BD所在直线的解析式为y＝－x＋2…5分
⑵在Rt△AOB中，AB＝
＝4，OA＝
＝6 ∵OB＝OC＝2 ∴AC＝AB－BC＝4－2＝2 …6分过点C作CE⊥OA于E，在Rt△ACE中，CE＝AC·sin∠OBA＝2×＝∴AE＝
＝3∴OE＝OA－AE＝6－3＝3…8分∴点C的坐标为(3，) …9分
31．⑴∵OA＝8，OB＝6，∴S△AOB＝×8×6＝24…2分
⑵∵OA＝8，OB＝6，∴AB＝＝10…3分当∠BPM＝∠AOB＝90°时∴△BPM∽△BOA ∴
∴
∴
秒…5分当∠BPM＝∠AOB＝90°时∴△BPM∽△BOA ∴
∴
∴
秒…7分∴当
秒或
秒时，△BPM与△BOA相似。…9分