浦东新区2005学年度第二学期期末抽测试卷
初二数学
一、填空题：（本大题共14题，每题3分，满分42分）
1．方程
的解是
．
2．如果一次函数y=kx-3的图象与正比例函数y=2x的图象互相平行，那么k= ．
3．如果关于x的方程
有两个相等的实数根，那么k的值等于
．
4．以3和-4为两根的一元二次方程是 ．
5．抛物线
的对称轴是直线
．
6．二次函数
的图象与y轴相交的交点坐标为
．
7．已知点A的坐标为（-1，4），点B的坐标为（3，1），那么线段AB的长等于 ．
8．已知矩形的长为5cm，宽为3cm，如果这个矩形的长和宽各增加x（cm），那么它的周长增加y（cm）．请写出y与x的函数解析式 ．
9．等腰三角形底边上的高等于腰长的一半，那么这个等腰三角形的顶角是 度．
10．已知四边形ABCD中，AC⊥BD，AC=4，BD=5，那么这个四边形的面积等于 ．
11．正方形的对角线长为10，那么这个正方形的周长是 ．
12．在半径为13的圆中，有两条长分别为10与24的弦互相平行，那么这两条平行弦之间的距离是 ．
13．如果顺次连结四边形ABCD各边中点所得四边形是矩形，那么这个四边形ABCD的对角线AC和BD的关系是 ．
14．到已知角两边距离相等的点的轨迹是 ．
二、选择题：（本大题共4题，每题2分，满分8分）
15．一次函数
的图象不经过…………………………………………………（ ）
（A）第一象限； （B）第二象限； （C）第三象限； （D）第四象限．
16．将二次函数
的图象向右平移4个单位，所得图象表示的函数解析式为……（ ）
（A）
； （B）
； （C）
； （D）
．
17．下列图形中，不一定是轴对称图形的是………………………………………………（ ）
（A）平行四边形； （B）等腰三角形； （C）等腰梯形； （D）圆．
18．下列命题中，假命题是………………………………………………………………（ ）
（A）菱形的对角线互相平分； （B）菱形的对角线互相垂直；
（C）菱形的对角线相等； （D）菱形的对角线平分一组对角．
三、（本大题共4题，每题6分，满分24分）
19．已知一次函数的图象经过点（-2，1）和（0，5），求这个一次函数的解析式．
20．解方程：
．
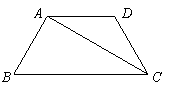
21．在等腰梯形ABCD中，AD∥BC，AB=CD=AD，AC⊥AB．求∠B的度数．
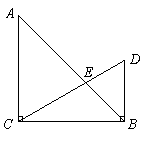
22．把一副直角三角板按如图形式叠放在一起，其中∠ACB=∠CBD=90°，AC=BC=10，
∠BCD=30°．求这副直角三角板重叠部分的面积．
四、（本大题共2题，每题8分，满分16分）
23．已知：如图，AD是△ABC的高，AB=AC，BE=2AE，点N是CE的中点．
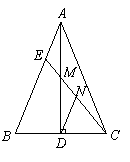求证：M是AD的中点．
24．已知关于x的方程
．
（1）求证：无论m取何实数值，方程总有两个实数根；
（2）如果Rt△ABC的斜边长为5，两条直角边长恰好是这个方程的两个根．求△ABC的面积．
五、（本大题只有1题，满分10分）
25．已知：一条抛物线的开口向上，顶点为A（-2，0），与y轴相交于点B，过点B作BC∥x轴，交抛物线于点C，过点C作CD∥AB，交x轴于点D．
（1）求点D的坐标．
（2）试探索：AC与BD能否互相垂直？如果能，请求出以这条抛物线为图象的二次函数的解析式；如果不能，请说明理由．
2005学年度第二学期期末抽测试卷初二数学
参考答案及评分说明
一、填空题：
1．0或3； 2．2； 3．5或-3； 4．
； 5．x=-3； 6．（0，4）；
7．5；8．y=4x； 9．120； 10．10； 11．
； 12．17或7；
13．互相垂直；
14．这个角的平分线．
二、填空题：
15．B； 16．D； 17．A 18．C．
三、
19．解：设所求一次函数的解析式为y=kx+b．…………………………………………（1分）
根据题意，得
………………………………………………………（2分）
解得
………………………………………………………………………（2分）
∴所求的一次函数解析式是y=2x+5．…………………………………………（1分）
20．解：去分母，得
．……………………………………………………（1分）
整理，得
．………………………………………………………（1分）
∴
．………………………………………（4分）
21．解：在等腰梯形ABCD中，
∵AD∥BC，AB=CD，∴∠B=∠BCD．…………………………………………（1分）
∵AD=CD，∴∠ACD=∠CAD．…………………………………………………（1分）
又∵AD∥BC，∴∠ACB=∠CAD．………………………………………………（1分）
∴∠ACB=∠ACD．………………………………………………………………（1分）
∵AC⊥AB，∴∠B+∠ACB =90°．……………………………………………（1分）
∴∠B+
∠B =90°．
∴∠B=60°．………………………………………………………………………（1分）
22．解：作EH⊥BC于点H，设EH=x．…………………………………………………（1分）
∵∠ACB =90°，AC=BC=10，∴∠ABC =45°．………………………………（1分）
∴BH=EH=x．
∵∠CBD =90°，∠BCD
=30°，∴CH=
x．………………………………（1分）
∴
．…………………………………………………………………（1分）
∴
．…………………………………………………………………（1分）
∴S△BCE=
． ……………………………………（1分）
四、
23．证明：∵AB=AC，AD⊥BC，∴BD=CD．……………………………………………（1分）
∵CN=EN，∴DN∥BE，DN=BE．……………………………………………（2分）
∵BE=2AE，∴DN=AE．…………………………………………………………（1分）
∵AE∥DN，∴∠MAE=∠MDN，∠MEA=∠MND．…………………………（1分）
∴△AEM≌△DNM．……………………………………………………………（2分）
∴AM=DM，即M是AD的中点．………………………………………………（1分）
24．（1）证明：∵
………………………………………………（1分）
，………………………………………………………（1分）
∴此方程总有两个实数根．………………………………………………（1分）
（2）解：设Rt△ABC的两条直角边分别为a、b．
根据题意，得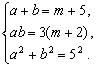 
………………………………………………（1分）
∴
．
∴
．…………………………………………………………（1分）
解得
，
（不符合题意，舍去）．……………………………（1分）
∴ab=12．………………………………………………………………………（1分）
∴S△ABC=
．……………………………………………………………（1分）
五、
25．解：（1）根据题意，得 点B、C关于直线x=-2对称，点B的横坐标为0，
∴点C的横坐标为-4．…………………………………………………………（1分）
∴BC=4．………………………………………………………………………（1分）
∵BC∥AD，CD∥AB，
∴四边形ABCD是平行四边形．………………………………………………（1分）
∴AD=4．
∴点D的坐标为（-6，0）．…………………………………………………（1分）
（2）能．……………………………………………………………………………（1分）
要使AC与BD互相垂直，必须使平行四边形ABCD是菱形，
即AB=BC=4．…………………………………………………………………（1分）
∵AO=2，∴
，即点B的坐标为（0，
）．…………………（1分）
设所求的二次函数的解析式为
．………………………………（1分）
代入点B的坐标，得
．
∴
．……………………………………………………………………（1分）
∴当二次函数的解析式为
时，AC⊥BD．………（1分）