八年级数学下期中考试

八年级数学下期中考试

班级________姓名________得分________

一、选择题（每小题2分，共26分）

1． 在，，，，，中，是分式的个数是（　　）

A.5　　　　　　　B.4　 　　　　　　　 C.3  　　　　　　 D.2

2. 如果双曲线，当x<0时，y随x的增大而增大，那么m的取值范围是（　）

A．m<0　　 B．　　 C．　　 D．

 

3．如图 所示，∠A=∠D=90º，AC与BD交于O，AB=CD=4，AO=3，则BD的长为（　 ）。

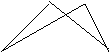A．6　　B．7　　C．8　　D．10　　　　　　　　　　 A　　　  D　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 O

　　　　　　　　　　　　　　　　　　　　　　　 C　　　　　　  B

4. 下列等式成立的是（　　）

A、　B、　C、　D、

5. 把分式中的分子分母的x、y都同时扩大为原来的2倍，那么分式的值将是原分式值的（　　）

A.2倍　　　　　　　B.4倍　　 　　　　C.一半　　 　　 D.不变

6．将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是(　　　)

A. 钝角三角形;　B. 锐角三角形;　C. 直角三角形;　D. 等腰三角形.

7. 某厂去年产值是m万元，今年产值是n万元（m＜n），则今年的产值比去年的产值增加的百分比是（　　）

A、B、CD

8．下列函数表达式中，均表示自变量，不是反比例函数的是（　　　）

　 A.　　  B.　 C.　　  D.

9．如图所示的图象的函数关系式只能是（　　 ）

A. 　　　　B.　　　 C. 　　　D.

10．男孩戴维是城里的飞盘冠军，戈里是城里最可恶的踩高跷的人，两人约定一比高低．戴维直立肩高1米，他投飞盘很有力，但需在13米内才有威力；戈里踩高跷时鼻子离地13米，他的鼻子是他惟一的弱点．戴维需离戈里(　　  )远时才能击中对方的鼻子而获胜．

A. 7米　　B．8米　　C.　6米　　D．5米

12．在函数(k＞0)的图象上有三点A₁(x₁, y₁ )、A₂(x₂, y₂)、A₃(x₃, y₃ ),已知x₁＜x₂＜0＜x₃,则下列各式中,正确的是 (　　)

　A.y₁＜y₂＜y₃　 　B.y₃＜y₂＜y₁　 C. y₂＜ y₁＜y₃D.y₃＜y₁＜y₂

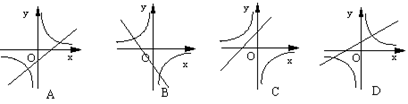
13.如图，函数y＝k（x＋k）与在同一坐标系中，图象只能是下图中的（　　）

二、填空题（每空2分，共28分）

14．不改变分式的值，使分子、分母的第一项系数都是正数，则.

15.木工做一个长方形桌面，量得桌面的长为60㎝，宽为32㎝，对角线为68㎝，这个桌面________（填“合格”或“不合格”）

16．已知－＝5，则的值是　　　 ．

17.　已知三角形的三边长分别为5、12、13，则此三角形面积为________

18．用科学记数法表示－0.=_____________________.

19．若分式的值为正，则的取值范围等于_____________.

2 0．点（，5）在反比例函数的图象上，则=_______，该反比例函数的图象位于第________象限，在每个象限内随的增大而__________.

21．A、B两地相距48千米，一艘轮船从A地顺流航行至B地，又立即从B地逆流返回A地，共用去9小时，已知水流速度为4千米/时，若设该轮船在静水中的速度为x千米/时，则可列方程_______________________________

22 已知，三角形的三边分别是13 、14、15，则三角形的面积是_____________

23. 点P在函数的图象上，A在X轴的正半轴上，O为坐标原点，PA=PO，∠APO=Rt∠，则△POA的面积=_____________________.

24．正比例函数的图象与反比例函数的图象的一个交点是A，点A的横坐标是2，则此反比例函数的关系式为_________________.

25．已知直线交轴于点A，交轴于点B，交双曲线于点D，DC⊥轴，垂足为C，且，则=_______________.

三、解答题（共56分）

26．（每小题4分，共16分）化简下列各式：

（1）　＋．　　　 　　　　　（2）.

（3）.　　　 （4）

27．（每小题4分，共8分）解下列方程：

（1）．　　　　　　　　 （2）

28.（6分）已知一次函数y=kx+b图像与反比例函数的图像相交于A和B点，点A的横坐标为3，点B的纵坐标是－3。

（1）求一次函数的解析式。

（2）当x为何值时，一次函数的值小于反比例函数的值。

29 印度数学家什迦逻（1141年-1225年）曾提出过“荷花问题”：

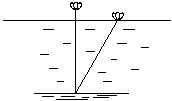“平平湖水清可鉴，面上半尺生红莲；

出泥不染亭亭立，忽被强风吹一边，

渔人观看忙向前，花离原位二尺远；

能算诸君请解题，湖水如何知深浅？”

请用学过的数学知识回答这个问题。（5分）

 

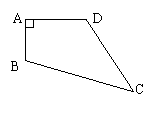
31(7分) 已知，如图，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，

且∠A=90°，求四边形ABCD的面积。

31．（7分）阅读材料题

对于题目“若方程的解是正数，求a的取值范围。”有同学作了如下解答：

解：去分母，得　

化简，得　

所以　　 

欲使方程的解为正数，必须，得

所以当时，方程的解是正数。

上述解法是否有误？若有错误，请指出错误原因，并写出正确解法；

若无错误，请说明每一步变形的依据。

32.（7分）某地上年度电价为0.8元，年用电量为1亿度，本年度计划将电价调至0.55~0.75元之间，经测算，若电价调至x元，则本年度新增用电量y（亿度）与元成反比例。又当x=0.65元时，y=0.8。

　　（1）求y与x之间的函数关系式。

（2）若每度电的成本价为0.3元，则电价调至多少时本年度电力部门的收益将比上年度增加20%？（收益=用电量×（实际电价－成本价））