初二下期期末数学综合复习资料（十）
一、 填空题（2×12＝24分）
1、
是__________的算术平方根。
2、每一个外角都是720的多边形的边数是______，这个多边形的内角和等于 度。
3、已知
，且
， 则
________。
4、
的倒数为 。
5、数轴上表示
的点到原点的距离等于_____________ 。
6、如图，在△ABC中，DE // BC，且AD＝1，BD＝2，则
________。
7、如图，平行四边形ABCD的周长为32cm，AB＝6cm，对角线BD＝8cm，则此平行四边形ABCD的面积为_______cm2
8、比较大小：
（填＞或＜）。
9、在Rt△ABC中，两条直角边长分别为6和8，则斜边上的中线为 。
10、一个等腰梯形的上底长为9cm，下底长为15cm，一个底角为60度，则其腰长为____cm
11、若
成立，则
的取值范围是____________。
二、 选择题（3×6＝18分）
12、一个数如果有两个平方根，那么这两个平方根的积必定（ ）
A、大于0 B、等于0 C、小于0 D、小于或等于0
13、下列各式计算正确的是（ ）
A、
B、
C、
D、
14、下面四个命题；
① 相邻的两个角都互补的四边形是平行四边形
② 对角线相等的四边形是矩形
③ 一组对边平行，另一组对边相等的四边形是平行四边形
④ 对角线互相垂直平分的四边形是菱形。
其中正确的是（ ）
A、①④ B、②④ C、②③ D、①③
15、如图，DE // FG // BC，且DE、FG把△ABC的面积三等份，若BC＝12cm，则FG的长（ ）
A、6cm B、8cm
C、
cm
D、 
cm
16 下列叙述错误的是 （ ）
A、被开方数不同的二次根式，一定不是同类二次根式；
B、同类二次根式不一定是最简二次根式；
C、判别同类二次根式，首先要把二次根式化成最简二次根式；
D、同类二次根式化成最简二次根式后被开方数一定相同；
17、在图形 ①线段；②角；③等腰三角形；④平行四边形；⑤菱形；⑥矩形中，既是轴对称图形又是中心对称图形的是（ ）
A、①③⑤ B、②③⑥ C、①⑤⑥ D、②④⑤
三、计算或化简（每小题4分，共20分）
18、计算
19、计算
20、化简：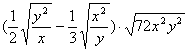
； 21、计算：
22、已知：
，
求
的值。
四、作图题。（本题满分5分）
23、如图，已知线段AB，在AB上求作点C、D，使得AC∶CD∶DB＝1∶2∶3
要求：①不写作法，保留作图痕迹
② 用一句话写明你作法的依据，并填在下面的横线上：作法的依据是
“_____________________ ___”定理
五、计算或证明：（5小题，共33分）
24、如图：△ABC中，BD、CE是两条高，AM是∠BAC的平分线，且交DE于N， 求证：
（6分）
25、如图，梯形ABCD中，AD // BC，AD＝3cm，BC＝10cm，EF // BC交AB、DC分别于E、F，且AE＝2EB。求线段EF的长（6分）
26、如图，梯形ABCD中，AD // BC，AB＝DC。
（1）如果P、E、F分别是BC、AC、BD的中点，求证：AB＝PE＋PF
（2）如果P是BC上的任意一点（中点除外），PE // AB， PF // DC，那么AB＝PE＋PF这个结论还成立吗？如果成立，请证明，如果不成立，请说明理由。（7分）
27、△ABC是一块直角三角形余料，∠B＝Rt∠，AB＝8cm，BC＝6 cm，如图将它加工成正方形零件，试说明哪种方法利用率高？（即得到的正方形面积较大）（8分）
（第十套）
一：1、
；2、5、5400；3、6；4、
；5、
；6、
；7、48；8、＜；
9、5；10、6；11、≥2
二、CCADA，C
三：18、
；19、
；20、
；21、－1；22、39
四：23、平行线分线段成比例定理
五：24、△AEC∽△ADB
AE·AB＝AD·AC△ADE∽△ABC
△ADN∽△ABM
△ADE∽△ABC
25、延长BA、CD相交于点G，设EB＝k，
AD∥BC
AD∥EF
26、①由三角形中位线定理可知PE＝
AB，PF＝DC，又∵AB＝DC ∴AB＝PE＋PF
②成立。
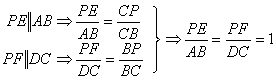；又∵AB＝DC ∴AB＝PE＋PF
27、设正方形的边长为cm。
（1）如图1，FE∥BC
（2）如图2，MQ∥AC△BMQ∽△BCA 
∵
＜
∴方案二利用率高。