初二下期期末数学综合复习资料（十一）
一、填空题（2×13＝26分）
1、
的平方根是________；
的立方根是_________。
2、已知
有意义，则
的取值范围是______________。
3、在
、
、
、
、
当中，___________________是无理数。
4、化简：
＝_____________
5、平方根等于
和
的数是 。
6、八边形的内角和等于___________度，外角和等于__________度。
7、平行四边形ABCD中，∠A∶∠B ＝ 2∶7，则∠C＝________。∠D＝_______。
8、顺次连结矩形四边中点所得的四边形是_________________。
9、一个菱形的面积是24cm2，一条对角线长是6cm，则其周长是________ cm。
10、直角梯形的高和上底长都是2cm，一个底角是300，则其面积为_______________。
11、如图，平行四边形ABCD的对角线相交于点O，AD＞CD，过点O作OE⊥BD交AD于E，已知△ABE的周长是
，则平行四边形ABCD的周长是_________。
12、设
，则
＝______ 。
二、选择题（每小题2分，共24分）
13、一个数的平方根等于这个数本身，这个数是（ ）
A、 1 B、 0 C、－1 D、0或－1
14、下列说法中不正确的是（ ）
A、实数包括有理数和无理数 B、无理数是无限小数
C、有理数是有限小数 D、绝对值最小的实数是0
15、下列各组数的比较中，错误的是（ ）
A、
＞
B、＞ 3.14 C、
＞
D、
16、下列计算正确的是（ ）
A、
B、
C、
D、
17、在①
；②
；③
；④
中，与
是同类二次根式的是（ ）
A、①和③ B、②和③ C、①和④ D、③和④
18、甲、乙两同学对
（＞0，
＞0）分别作了如下变形：
甲：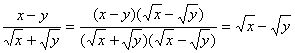
乙：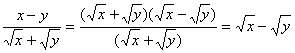
关于这两种变形过程的说法正确的是（ ）
A、只有甲正确 B、只有乙正确 C、甲乙都正确 D、甲乙都不正确
19、能判定一个四边形是平行四边形的条件是（ ）
A、一组对边平行，另一组对边相等 B、一组对边平行，一组对角相等
C、一组对边相等，一组对角相等 D、两组邻角互补
20、下列图形中是中心对称图形而不是轴对称图形的是（ ）
A、线段 B、平行四边形 C、矩形 D、菱形
21、如图，
，另两条直线分别与其相交于点A、C、E和B、D、F，则下列式子中不一定成立的是（
）
A、
B、
C、
D、
22、如图，要使△ABC∽△BDC，必须具备的条件是（ ）
A、
B、
C、
D、
23、如图，平行四边形ABCD中，E是BC的中点，F是BE的中点，AE、DF交于点H，则
与
的比值是（ ）
A、
B、
C、
D、
三、解答题：（前3题每题4分，后2题每题5分，共22分）
24、已知
≈1.414，≈1.732，求
的值。（精确到0.01）
25、计算：
26、
27、若
，
，求
的值。
28、若＞
＞0，
。求
的值。
四、解答或证明题（本题共28分）
29、在梯形ABCD中，AD // BC，DB⊥DC，AD＝AB＝DC。
（1）求∠A、∠C的度数。 （2）若AD＝2cm，求它的中位线长和面积。（5分）
30、如图，过平行四边形ABCD的顶点D作直线交BC于F，交AB的延长线于E。求证：
（5分）
31、如图，Rt△ABC中，∠ACB＝900，D、E分别是AB、AC的中点，点F在BC的延长线上，且∠CEF＝∠A。
（1）求证：DE＝CF
（2）若BC＝2，AB＝6，求四边形DCFE的周长。
32、如图，四边形ABCD中，∠ABC＝∠ADC＝900，过点C作MN⊥AC分别交AB、AD的延长线于M、N，试判断∠M与∠ADB有何关系？并证明你的结论。（6分）
33、请按下列步骤折叠矩形纸片ABCD：（6分）
（1）折出折痕AC（对角线）
（2）通过折叠使AB与对角线AC重合，得折痕AG，若AB＝1，BC＝2，求BG的长。
（第十一套）
一：1、±3、
；2、≥
；3、、；4、
；5、49提示：
；6、10800、3600；7、400、1400；8、菱形；9、20
10、
cm2；11、
；12、1或－2。
二、BCDDC，CBBDC，D
三：24、1.28；25、
；26、
；
27、原式＝
＝
＝
； 28、
。
四：29、①∠A＝1200、∠C＝600；②中位线长3cm、面积
cm2。
30、平行四边形ABCD
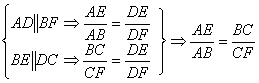；又因为BC＝AD
∴
31、①证△ADE≌△EFC（ASA）；
②利用三角形中位线定理和勾股定理可求出周长为8。
32、答：相等。
∵CB是Rt△ACM斜边上的高
∴AC2＝AB·AM 同理AC2＝AD·AN
∴AB·AM＝AD·AN
∴△ABD∽△ANM
∴∠M＝∠ADB
33、过D作DE⊥AC于E，可证△ABG≌△AEG得：AB＝AE＝1，BG＝GE＝
在Rt△EGC中，∵EG2 ＋EC2＝GC2 ∴
∴