八年级下学期单元测试四(相似图形B卷)

一、选择题:本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 如图,下列条件中不能判定![]() 的是( )
的是( )
(A)![]() (B)
(B)![]()
 (C)
(C)![]() (D)
(D)![]()
2. 下列两个图形一定相似的是 .
A.三角形与四边形 B.两个正五边形
C.两个六边形 D.两个四边形
3. 若![]() ,则下列式子中正确的是
,则下列式子中正确的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. 若![]() 则
则![]() 的值为
的值为
(A)![]() (B)
(B)![]()
 (C)
(C)![]() (D)
(D)![]()
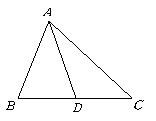
5.  如图,
如图,![]() 是Rt
是Rt![]() 的斜边
的斜边![]() 上异于
上异于![]() 、
、![]() 的一点,过
的一点,过![]()
点作直线截![]() ,使截得的三角形与
,使截得的三角形与![]() 相似,满足这样条件
相似,满足这样条件
的直线共有( )条
A.1 B.2 C.3 D.4
6. 已知![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
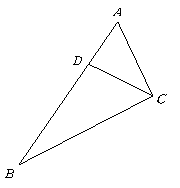
7. 如图,![]() 为
为![]() 的边
的边![]() 上的一点,连接
上的一点,连接![]() ,要使
,要使![]() ,应具备下列条件中的( )
,应具备下列条件中的( )
A.![]() B.
B.![]()
 C.
C.![]() D.
D.![]()
8. 下列各组线段中,能成比例的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
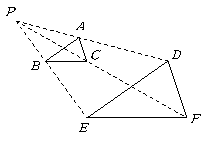
9. 如图,将![]() 缩小为原来的一半,操作方法如下:任意取一点
缩小为原来的一半,操作方法如下:任意取一点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,再连接
,再连接![]() ,取它们的中点
,取它们的中点![]() ,得到
,得到![]() ,则下列说法正确的有( )
,则下列说法正确的有( )
①![]() 与
与![]() 是位似图形;
是位似图形;
②![]() 与
与![]() 是相似图形;
是相似图形;
③![]() 与
与![]() 的周长比是1:2;
的周长比是1:2;
④![]() 与
与![]() 的面积比是1:2.
的面积比是1:2.
(A)1个 (B)2个
(C)3个 (D)4个
 |
10. 如果两个等腰直角三角形斜边的比是![]() ,那么它们面积的比为( )
,那么它们面积的比为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题:本大题共5小题,每小题3分,共15分,把答案填写在题中横线上.
11. 两个矩形相似,它们的对角线之比为![]() ,那么它们的相似比为 ,周长比为 ,面积比为 .
,那么它们的相似比为 ,周长比为 ,面积比为 .
12. 若![]() ,则
,则![]() .
.
13. 两个相似五边形的相似比为![]() ,则它们的周长的比为 .
,则它们的周长的比为 .
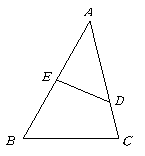
14. 如图,在![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,且
上,且![]() ,若
,若![]() cm,则
cm,则![]() cm.
cm.
 |
15. 已知![]() ,则
,则![]() ;
;![]() ;
;![]() .
.
三、运算题:本大题共3小题,共15分,解答应写出必要的计算过程、推演步骤或文字说明.
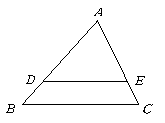
16.(本小题5分) 如图,如果![]() ,那么
,那么![]() 与
与![]() 的比值是否相等?请说明理由.
的比值是否相等?请说明理由.
 |
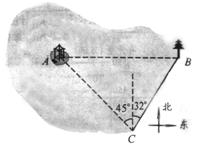
17.(本小题5分) 小胖和小瘦去公园玩标准的跷跷板游戏,两同学越玩越开心,小胖对小瘦说:“真可惜!
我只能将你最高翘到1米高,如果我俩各边的跷跷板都再伸长相同的一段长度,那么我
就能翘到1米25,甚至更高!”
(1)你认为小胖的话对吗?请你作图分析说明;
(2)你能否找出将小瘦翘到1米25高的方法?试说明.
 解:
解:
18.(本小题5分) 解答题.
(1)在平面直角坐标系描出点![]() ,顺次连结点
,顺次连结点![]() 得到一个五边形
得到一个五边形![]() .
.
(2)将点![]() 的横坐标和纵坐标都除以2,得到五个新的点,顺次连结这五个点,得到一个新的五边形,这两个五边形相似吗?是位似图形吗?为什么?
的横坐标和纵坐标都除以2,得到五个新的点,顺次连结这五个点,得到一个新的五边形,这两个五边形相似吗?是位似图形吗?为什么?
如果将点![]() 的横坐标和纵坐标都乘以3呢?
的横坐标和纵坐标都乘以3呢?
四、画图题:本大题共2小题,共10分,解答应写出必要的计算过程、推演步骤或文字说明.
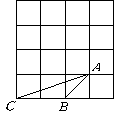
19.(本小题5分) 如图,在大小为![]() 的正方形网格上,有一
的正方形网格上,有一![]() ,现要求在网格上再画
,现要求在网格上再画![]() ,使
,使![]() (相似比不为1),且点
(相似比不为1),且点![]() 都在单位正方形的顶点上.
都在单位正方形的顶点上.
 |
20.(本小题5分) 如图,作出一个新图形,使新图形与原图形对应线段的比为2:1.
 | |||
 | |||
五、合情推理题:本大题共2小题,共16分,解答应写出必要的计算过程、推演步骤或文字说明.
21.(本小题8分) 如下图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,请观察下面图形并回答有关问题:
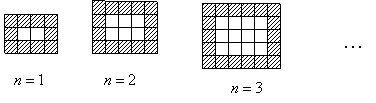 |
(1)在第![]() 上图中,每一横行共有 块瓷砖,每一竖行共有 块瓷砖.(均用含
上图中,每一横行共有 块瓷砖,每一竖行共有 块瓷砖.(均用含![]() 的代数式表示)
的代数式表示)
(2)设铺设地面所用瓷砖的总块数为![]() ,请写出
,请写出![]() 与(1)中的
与(1)中的![]() 的函数关系式.(不要求写自变量
的函数关系式.(不要求写自变量![]() 的取值范围)
的取值范围)
(3)按上述铺设方案,铺一块这样的矩形地面共用了506块瓷砖,求此时![]() 的值.
的值.
(4)若黑瓷砖每块4块,白瓷砖每块3元,在问题(3)中,共须花多少元钱购买瓷砖?
(5)通过计算说明,是否存在黑瓷砖与白瓷砖块数相等的情形.
22.(本小题8分) 你能用4个全等的正三角形拼出一个大正三角形吗?这个大正三角形与每一个小正三角形相似吗?为什么?
六、证明题:本大题共2小题,共14分,解答应写出必要的计算过程、推演步骤或文字说明.
23.(本小题7分) 已知:如图,等腰![]() 中,
中,![]() 交于
交于![]() ,
,![]() ,
,![]() 分别交
分别交![]() 于
于![]() .
.
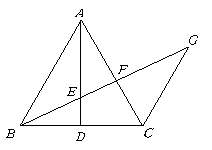 求证:
求证:![]()
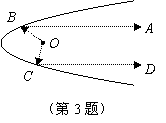
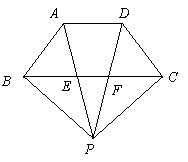
24.(本小题7分) 如图,梯形![]() 中,
中,![]() ,
,![]() 为梯形
为梯形![]() 外一点,
外一点,![]() 、
、![]() 分别交线段
分别交线段![]() 于点
于点![]() 、
、![]() ,且
,且![]() .
.
(1) 写出图中三对你认为全等的三角形(不再添加辅助线);
(2) 选择你在(1)中写出的全等三角形中的任意一对进行证明.
 |
参考答案

一、选择题:本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. (A)
2. B
3. D
4. A
5. C
6. A
7. B
8. C
9. (C)
10. (D)
二、填空题:本大题共5小题,每小题3分,共15分,把答案填写在题中横线上.
11. ![]()
![]()
![]()
12. ![]()
13. ![]()
14. 6
15. ![]()
三、运算题:本大题共3小题,共15分,解答应写出必要的计算过程、推演步骤或文字说明.
16.(本小题5分) 相等.理由略.
17.(本小题5分) 解:(1)小胖的话不对.
小胖说“真可惜!我现在只能将你最高翘到1
米高”,情形如图(1)所示,![]() 是标准跷跷
是标准跷跷
板支架的高度,![]() 是跷跷板一端能翘到的最
是跷跷板一端能翘到的最
高高度1米,![]() 是地面.
是地面.
![]()
![]()
又![]() 此跷跷板是标准跷跷板,
此跷跷板是标准跷跷板,![]() ,
,
![]() 而
而![]() 米,得
米,得![]() 米.
米.
 若将两端同时都再伸长相同的长度,假设为
若将两端同时都再伸长相同的长度,假设为![]() 米
米![]() .
.
如图(2)所示,![]() 米,
米,![]() 米
米
![]() ,即
,即![]() .
.
![]() ,同理可得
,同理可得![]() .
.
![]() ,由
,由![]() 米,得
米,得![]() 米.
米.
 |
综上所述,跷跷板两边同时都再伸长相同的一段长度,
跷跷板能翘到的最高高度始终为支架![]() 高度的两倍,
高度的两倍,
所以不可能翘得更高.
(2)方案一:如图(3)所示,保持![]() 长度不变.将
长度不变.将
![]() 延长一半至
延长一半至![]() ,即只将小瘦一边伸长一半.
,即只将小瘦一边伸长一半.
使![]() 则
则![]() .
.
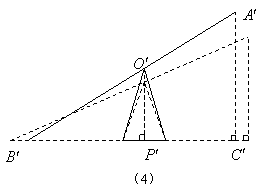 由
由![]() 得
得![]()
![]() 米.
米.
方案二:如图(4)所示,只将支架升高0.125米.
![]()
又![]() 米.
米.
![]() .
.
![]() 米.
米.
(注:其它方案正确,可参照上述方案评分!)
18.(本小题5分) 略
四、画图题:本大题共2小题,共10分,解答应写出必要的计算过程、推演步骤或文字说明.
19.(本小题5分) 略
20.(本小题5分) 略
五、合情推理题:本大题共2小题,共16分,解答应写出必要的计算过程、推演步骤或文字说明.
21.(本小题8分) (1)![]() ,
,![]() .
.
(2)![]() ,即
,即![]() .
.
(3)当![]() 时,
时,![]() ,即
,即![]() ,
,![]() ,
,![]() (舍去).
(舍去).
(4)白瓷砖的块数是![]() ,黑瓷砖的块数是
,黑瓷砖的块数是![]() (块),故共须花
(块),故共须花![]() (元).
(元).
(5)由![]() 得
得![]() ,得
,得![]() ,
,![]() (舍去),
(舍去),![]() 的值不是正整数,
的值不是正整数,![]() 不存在黑、白瓷砖块数相等的情形.
不存在黑、白瓷砖块数相等的情形.
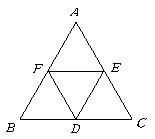
22.(本小题8分) 解:能并出一个大正三角形,如图所示:
![]() .
.
下面以![]() 为例说明:
为例说明:
由于正三角形每个角都等于![]() ,
,
所以![]()
![]()
由于正三角形三边相等,
所以![]() .
.
所以![]() .
.
 |
六、证明题:本大题共2小题,共14分,解答应写出必要的计算过程、推演步骤或文字说明.
23.(本小题7分) 证明:连接![]() .
.
证明![]() 与
与![]() 相似.
相似.
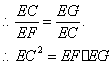
又![]() ,
,
![]() .
.
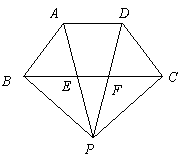
24.(本小题7分) (1)以下四对.
①![]() ;②
;②![]() ;③
;③![]() ;
;
④![]() .
.
 (2)下面就
(2)下面就![]() 给出参考答案.
给出参考答案.
证明:![]()
![]() 梯形
梯形![]() 为等腰梯形,
为等腰梯形,
![]() .
.
又![]() ,
,
![]()
即![]()
在![]() 和
和![]() 中,
中,
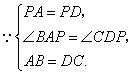
|