阳光中学第六次周周清试卷
————迎抽考模拟考试
一、
选择题：（每题3分，共60分）
1、下列各式：
，
，
，
，
，
中，是分式的共有（ ）
A、1个 B、2个 C、3个 D、4个
2、化简
的结果是（ ）
A、
B、
C、
D、
3、计算
的正确结果是（ ）
A、0
B、
C、
D、
4、根据分式的基本性质，分式
可变形为（
）
（A）
（B）
（C）
（D）
5、使分式
的值是负数
的取值范围是（ ）
（A）
（B）
（C）
（D）不能确定的
6、用科学记数法表示-0.000 0064记为（ ）
A、-64×10-7 B、-0.64×10-4 C、-6.4×10-6 D、-640×10-8
7、若关于x的分式方程
有增根，则m的值为( )
A、0 B、1 C、2 D、3
8、甲从A地到B地要走m小时，乙从B地到A地要走n小时，若甲、乙二人同时从A、B两地出发，经过几小时相遇( )
A、(m＋n)小时
B、
小时 C、
小时 D、
小时
9.若m＜1,则下列函数①y＝
;②y＝－mx＋1;③y＝－(x＞0); ④y＝(m＋1)x中,y随x增大而增大的有( )
A.1个 B.2个 C.3个 C.4个
10. 在反比例函数y＝
－
的图象上有三点(x1,y1) ，(x2,y2)
，(x3,y3) , 若x1＞x2＞0 ＞x3 ,则下列各式正确的是( )
A. y3 ＞y1 ＞y2 B. y3 ＞y2 ＞y1
C. y1 ＞y2 ＞ y3 D. y1 ＞y3＞ y2
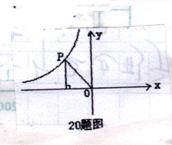11.如图7,P(a,b)在反比例函数y＝
(k≠0)的图象上,且a,b是函数t2－t－12＝0的两根,过P作PA⊥x轴于点A,则△PAO的周长是( )
A.7 B.10 C.11 D.12
12. 函数
与
的图象可能是（ ）
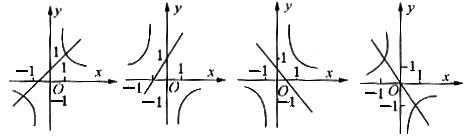
A B C D
13、下列说法不正确的是（ ）
（A）三个角的度数之比为1：3：4的三角形是直角三角形
（B）三个角的度数之比为3：4：5的三角形是直角三角形
（C）三边长度之比为3：4：5的三角形是直角三角形
（D）三边长度之比为5：12：13的三角形是直角三角形
14、一个圆桶底面直径为24cm，高32cm，则桶内所能容下的最长木棒为（ ）
（A）20cm (B)50cm (C)40cm (D)45cm
15、一职工下班后以50米/分的速度骑自行车沿着东西马路向东走了5.6分，又沿南北向马路向南走了19.2分到家，则他的家离公司距离为（ ）米。 （A）100 （B）500 （C）1240 （D）1000
16、有以下4上命题：①两条对角线互相平分的四边形是平行四边形；②两条对角线互相垂直的四边形是正方形；③两条对角线相等的四边形是菱形；④两条对角线相等且互相垂直的四边形是正方形。其中正确命题的个数是（ ）
A、1 B、2 C、3 D、4
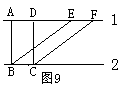
17、如图9所示， 1∥
2，BE∥CF，BA⊥
1，DC⊥
2，下面给出的四个结论：⑴AB=CD；⑵BE=CF；⑶S△ABE=S△DCF；⑷S□ABCD=S□BCFE，其中正确的有（ ）
A、4个 B、3个 C、2个 D、1个
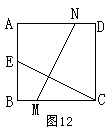
18、如图12，四边形ABCD是正方形，CE=MN，∠MCE=35o则∠ANM=（ ）
A、45o B、55o C、65o D、75o
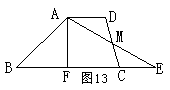19、如图13，梯形ABCD中，AD∥BC，AF⊥BC，M是CD的中点，∠B=45o，AF=4，EF=7，则梯形ABCD的面积（ ）
A、22 B、24 C、26 D、28
20、对角线互相垂直且相等的四边形是 （ ）
A、菱形 B、矩形 C、正方形 D、以上结论都不对
二、计算题：（每题5分，共40分）
1、
。
2、先化简，再求值：
，其中：x=－2。
3 、（8分）解分式方程：
。
4、（10分）一名同学计划步行30千米参观博物馆，因情况变化改骑自行车，且骑车的速度是步行速度的1.5倍，才能按要求提前2小时到达，求这位同学骑自行车的速度。
5. 直线过x轴上的点A（
，0），且与双曲线
相交于B、C两点，已知B点坐标为（
，4），求直线和双曲线的解析式。
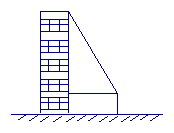6、一高层住宅发生火灾，消防车立即赶到距大厦9米处（车尾到大厦墙面），升起云梯到火灾窗口，已知云梯长15米，云梯底部距地面2米，问：发生火灾的住户窗口距离地面多高？（10分）
7、已知，如图15，AD是△ABC的角平分线，DE∥AC交AB于点E，DF∥AB交AC于点F，求证：AD⊥EF (9分)
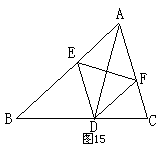
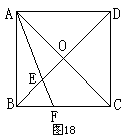
8、如图18，O是正方形ABCD的对角线的交点，AF平分∠BAC交BC于F，交BO于E，求证：OE= CF (8分)
