勾股定理期末复习试卷
一．知识技能
1. 有五组数：①7，24，25；②12，16，20；③9，40，41；④4，6，8；⑤32,42,52，以各组数为边长，能组成直角三角形的个数为( ).
A.2 B.3 C.4 D.5
2. 下列几组数中,不能作为直角三角形三边长度的是 ( )
A. a=7, b=24, c=25 B.
a=1.5, b=2, c=2.5
C. a=
, b=2, c=
D.
a=15, b=8, c=17
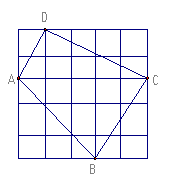
3. 如图小方格都是边长为1的正方形,则四边形ABCD的面积是 ( )
A. 25 B. 12.5 C. 9 D. 8.5
4. 如果梯子的底端离建筑物5米,13米长的梯子可以达到该建筑物的高度是 ( )
A. 12米 B. 13 C. 14米 D. 15米
5. 小强量得家里新购置的彩电荧光屏的长为58厘米,宽为46厘米,则这台电视机的尺寸 (对角线长，实际测量的误差可不计) 是 ( )
A. 9英寸(23厘米) B. 21英寸(54厘米) C. 29英寸(74厘米) D. 34英寸(87厘米)
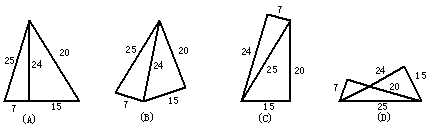
6、五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（ ）
7.如图，已知正方形的面积为25，且AB比AC大1，BC的长为( ).
A.3 B.4 C.5 D.6
8．若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( ) A. 12 cm B. 10 cm C. 8 cm D. 6 cm
9．三角形的三边长为（a+b）2=c2+2ab,则这个三角形是( )
A. 等边三角形; B. 钝角三角形; C. 直角三角形; D. 锐角三角形.
10. 直角三角形的两条直角边长为a,b,斜边上的高为h,则下列各式中总能成立的是 ( )
A. ab=h2 B. a
+b=2h
C. 
+
=
D. 
+
=
11．已知一个Rt△的两边长分别为3和4，则第三边长的平方是
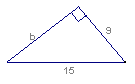
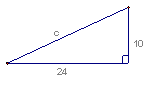
12． 求图中直角三角形中未知的长度:b=__________,c=____________.
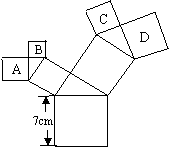
13．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm,则正方形A，B，C，D的面积之和为___________cm2。
14．已知三角形的三边长分别是2n+1,2n+2n, 2n+2n+1（n为正整数）则最大角等于_________度.
15 .观察下列表格：
| 列举 | 猜想 |
| 3、4、5 | 32=4+5 |
| 5、12、13 | 52=12+13 |
| 7、24、25 | 72=24+25 |
| …… | …… |
| 13、b、c | 132=b+c |
请你结合该表格及相关知识，求出b、c的值.
即b= ，c=
16．如果一个直角三角形的三边为三个连续偶数，那么它的三边长为 .
17．
已知
,则由此
为三边的三角形的面积是 _________ .
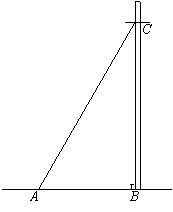
18．如图，要从电线杆离地面8m处向地面拉一条长10m的电缆，求地面电缆固定点A到电线杆底部B的距离.(6分)
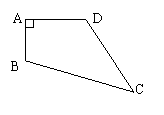19．已知，如图，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，且∠A=90°，求四边形ABCD的面积。
20．如图，在边长为c的正方形中，有四个斜边为c的全等直角三角形，已知其直角边长为a，b.利用这个图试说明勾股定理?
21. 如图，有一个直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上,且与AE重合,你能求出CD的长吗？
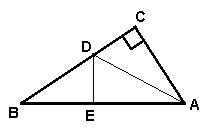
22.
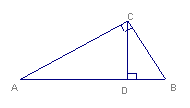
如图在Rt
中，CD是AB边上的高，若AD=8，BD=2 ，求 CD的长。
23．在中，AB=15，AC=13，BC边上的高AD=12，试求的周长。
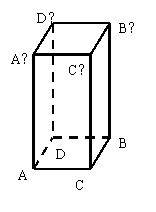24．一只蚂蚁如果沿长方体的表面从A点爬到B’点,那么沿哪条路最近,最短的路程是多少?已知长方体的长2cm、宽为1cm、高为4cm.
参考答案：1~~10 ：BCBAC CADCD
11：7或25， 12：12，26， 13：49， 14：90 0 ， 15：84，85，
16：6，8，10， 17：6， 18：6m， 19：36， 20：略， 21：1．75
22：4, 23：14或4, 24：5cm.
初二（下）期末能力特训综合 答案
1~10 ： D，Ｃ，Ｄ，Ｂ，Ｃ， Ｄ，Ｃ，Ｄ，Ｄ，Ｄ。
11：－２， 12： 20， 13：A， 14：600，1200， 15：1， 16：3，
17：4，2， 18：12， 19：16， 20：2，2， 21：x+9，11， 22：x=2，方程无解。23：略 24：A（—2，4），B（4，—2），6。