第19章 四边形单元复习测试
一、选择题
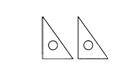
1.如图1,用两个完全相同的直角三角板,不能拼成下列图形的是( ).
A.平行四边形 B.矩形 C.等腰三角形 D.梯形
|
2.下列说法中,正确的是( ).
A.等腰梯形的对角线互相垂直 B.菱形的对角线相等
C.矩形的对角线互相垂直;
D.正方形的对角线互相垂直且相等
3.已知四边形ABCD是平行四边形,下列结论中,错误的是( ).
A.AB=CD; B.AC=BD; C.当AC⊥BD时,它是菱形; D.当∠ABC=90°时,它是矩形
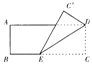
4.如图2,将一张矩形纸片ABCD那样折起,使顶点C落在C′处,其中AB=4,若∠C′ED=30°,则折痕ED的长为( ).
A.4 B.4![]() C.5
C.5![]() D.8
D.8
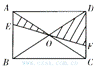
5.如图3,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形面积的( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
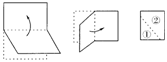
6.将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①,②两部分,将①展开后得到的平面图形是( ).
A.三角形 B.矩形 C.菱形 D.梯形
7.已知等腰梯形ABCD的中位线EF的长为6,腰AD的长为5,则等腰梯形的周长为( ).
A.11 B.16 C.17 D.22
8.顺次连结菱形各边中点所围成的四边形是( ).
A.一般的平行四边形 B.矩形 C.菱形 D.等腰梯形
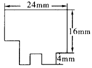
9.如图4是一块电脑主板的示意图,每一转角处都是直角,数据如图所示,则该主板的周长是( ).
A.88mm B.96mm C.80mm D.84mm
(4) (5) (6)
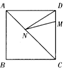
10.如图5,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( ).
A.8 B.8![]() C.2
C.2![]() D.10
D.10
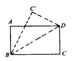
![]() 11.如下图3, ABCD中,AE平分∠DAB,∠B=100°,则
11.如下图3, ABCD中,AE平分∠DAB,∠B=100°,则
∠DAE等于( ).
A.100° B.80° C.60° D.40°
12.某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到设计方案有等腰三角形、正三角形、等腰梯形、菱形等四种图案,你认为符合条件的是( ).
A.等腰三角形 B.正三角形 C.等腰梯形 D.菱形
13.一个多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发的对角线的条数是( ).
A.6条 B.7条 C.8条 D.9条
14.如下图4,图中的△BDC′是将矩形ABCD沿对角线BD折叠得到的,图中(包括实线、虚线在内)共有全等三角形( )对.
A.1 B.2 C.3 D.4
二、填空题
1.如图1,DE∥BC,DF∥AC,EF∥AB,圈中共有_______个平行四边形.
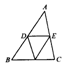
![]()
![]()
(1) (2) (3) (4)
2.如果边长分别为4cm和5cm的矩形与一个正方形的面积相等,那么这个正方形的边长为______cm.
3.已知菱形两条对角线的长分别为5cm和8cm,则这个菱形的面积是______cm.
4.平行四边形ABCD,加一个条件_________,它就是菱形.
5.如图2,长方形ABCD是篮球场地的简图,长是28m,宽是15m,则它的对角线长约为________m.(精确到1m)
![]() 6. ABCD两邻角∠A:∠B=1:2,则∠C=_____度.
6. ABCD两邻角∠A:∠B=1:2,则∠C=_____度.
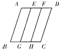
![]() 7.如图6,在 ABCD中,E、F和G、H分别是AD和BC的三等分点,则图中平行四边形的个数共有______个.
7.如图6,在 ABCD中,E、F和G、H分别是AD和BC的三等分点,则图中平行四边形的个数共有______个.
![]() 8.已知, ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于E,则DE=_____cm.
8.已知, ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于E,则DE=_____cm.
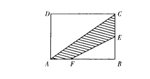 9.如图,在长方形ABCD中,AB=3,BC=2,E为BC的中点,F在AB上,且BF=2AF,则四边形AFEC的面积为________.
9.如图,在长方形ABCD中,AB=3,BC=2,E为BC的中点,F在AB上,且BF=2AF,则四边形AFEC的面积为________.
10.如图,矩形纸片ABCD中,AB=6cm,AD=9cm,再按以下步骤折叠:①将∠BAD对折,使AB落在AD上,得折痕AF(如图2);②将△AFB沿BF折叠,AF与CD交于点G(如图3),则CG的长等于_______cm.
11.过边长为1的正方形的中心O引两条互相垂直的射线,分别与正方形的边交于A、B两点,则线段AB长的取值范围是_______.
12.已知菱形ABCD的边长为6,∠A=60°,如果点P是菱形内一点,且PB=PD=2![]() ,那么AP的长为_______.
,那么AP的长为_______.
13.下面图1的梯形符合_______条件时,可以经过旋转和翻折成图案2.
三、简答题
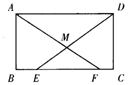 1.如图,在矩形ABCD中,点E、F在BC边上,且BE=CF,AF、DE交于点M.
1.如图,在矩形ABCD中,点E、F在BC边上,且BE=CF,AF、DE交于点M.
求证:AM=DM.(6分)
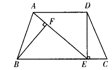
2.如图,等腰梯形ABCD中,AD∥BC,AB=CD,DE⊥BC于E,AE=BE.BF⊥AE于F,请你判断线段BF与图中的哪条线段相等,先写出你的猜想,再加以证明.(6分)
(1)猜想:BF=______.
(2)证明:
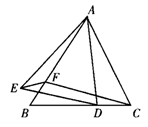
3.如图,△ABC为等边三角形,D、F分别是BC、AB上的点,且CD=BF,以AD为边作等边△ADE.
(1)求证:△ACD≌△CBF;
(2)当D在线段BC上何处时,四边形CDEF为平行四边形,且∠DEF=30°?证明你的结论.
4.如图,以△ABC的各边向同侧作正△ABD,BCF,ACE.
(1)求证:四边形AEFD是平行四边形;
(2)当△ABC是_____三角形时,四边形AEFD是菱形;
(3)当∠BAC=_____时,四边形AEFD是矩形;
(4)当∠BAC=_______时,以A、E、F、D为顶点的四边形不存在.
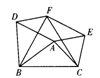
5.矩形,菱形由于其特殊的性质,为拼图提供了方便,因而墙面瓷砖一般设计为矩形,图案也以菱形居多.如图,是一种长30cm,宽20cm的矩形瓷砖,E、F、G、H分别是矩形各边的中点,阴影部分为淡黄色,中间部分为白色,现有一面长4.2m,宽2.8m的墙壁准备贴瓷砖.
问:(1)这面墙壁最少要贴这种瓷砖多少块?
(2)全部贴满瓷砖后,这面墙壁最多会出现多少个面积相等的菱形?其中淡黄色的菱形有多少个?
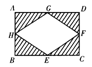
6.设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…….
(1)记正方形ABCD的边长为a1=1,按上述方法所作的正方形的边长依次为a2,a3,a4,……,an,请求出a2,a3,a4的值.
(2)根据以上规律写出an的表达式.(8分)
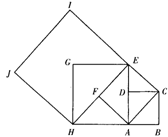
7.在一个平行四边形中若一个角的平分线把一条边分成长是2cm和3cm的两条线段,求该平行四边形的周长是多少?
8.如图,把一张长方形ABCD的纸片沿EF折叠后,ED与BC的交点为G,点D、C分别落在D′、C′的位置上,若∠EFG=55°,求∠AEG和∠ECB的度数.
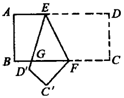
9.如图,一块正方形地板由全等的正方形瓷砖铺成,这地板的两条对角线上的瓷砖全是黑色,其余的瓷砖是白色的,如果有101块黑色瓷砖,那么瓷砖的总数是多少?
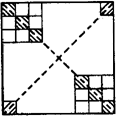
10.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由?
(2)当点O运动何处时,四边形AECF是矩形?并说出你的理由.
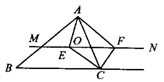
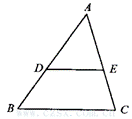
11.如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=![]() BC.根据上面的结论:
BC.根据上面的结论:
(1)你能否说出顺次连结任意四边形各边中点,可得到一个什么特殊四边形?并说明理由.
(2)如果将(1)中的“任意四边形”改为条件是“平行四边形”或“菱形”或“矩形”或“等腰梯形”,那么它们的结论又分别怎样呢?请说明理由.