八年级下第一次月考测试卷 2005.4
班级： 姓名： 学号：
一．选择题（每题3分，共24分）
1. 下列各式正确的是 （ ）
A. =±6 B. - = -2 C. = - 6 D. = -
2. 下列说法正确的是（ ）
A.3是9的平方根 B. - 9的平方根是±3 C.4的平方根是2 D.(-5)2的算术平方根是 -5
3. 如果
有意义，则
的取值范围为
（ ）
A.<2 B.≤2 C.>-2且≠-1 D. ≤2且≠-1
4. 如果
那么
（ ）
A．ｘ＞０ B.ｘ
５
C . 不存在 D. 以上都不对
5. 下列给出的四个点中，不在直线y = 2x - 3上的是 （ ）
A.（1， -1） B.（0， -3） C.（2， 1） D.（-1，5）
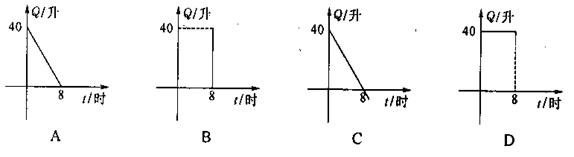
6. 汽车开始行驶时，油箱内有40升油，则油箱内剩余油量Q（升）与行驶时间t（时）的函数关系式为
（ ）
7. 若反比例函数y=，y随x的增大而减小，则m的取值范围是 （ ）
A. m > B. m < C.m > - D. m < -
8. 小明的父亲饭后散步，从家中走20分钟到一个离家900米的报亭看10分钟的报纸后，用15分钟返回家中，下列图形中表示小明父亲离家的时间x与距离y之间的关系是（ ）
A B C D
 |
二、填空题(每题2分，共30分)
9. = ,64的立方根为 。
10. 若 = 5,则x = ,平方根得10的数是 。
11. 算术平方根等于它本身的数是 ,立方等于它本身的数是 。
12. 如 
是同类二次根式，则a = ，b = 。
13. 若整数x满足关系式 < x < ,则x = 。
14. 在实数,,0.3,, ,,1-中,无理数有 。
15. 如果(x+1)2 + = 0 ,则x + 2y = 。
16. 我们已经知道是一个无理数,请写出三个比还要小的正无理数,其中一个是不带根号的无理数: 。
17. 的平方根是 。
18. 函数y =中自变量x的取值范围是 。
函数
中自变量x的取值范围是
。
19. 点A(a,-5)和(3,b)关于x轴对称,则a = ,b = 。
20. 茶叶蛋每个0.55元,小明和同学们一起买的茶叶蛋个数x与所付出的钱数y(元)之间的函数关系式为 ,变量x的取值范围是 .
21. 一次函数y =（2-k）x + 2（k为常数），y随x的增大而增大，则k的取值范围是 .
22. 点P（3－a，5－a）是第二象限的点，则a的取值范围是 。
23. 在一次函数y=(a+2)x+8的图象上有一点P,且点P的坐标为(-1,2),则a = 。
三、化简与求值
24.计算（12分）
⑴ - - ⑵ ( 1 - 2 )2
⑶ 3- · +
⑷ 
；
四、解答题
25.（6分）已知两个一次函数y = 4 x – 6 与y = - x + 6的图像与ｘ轴分别交于A、C两点，且这两个函数的图像交点为E，求：
（１）交点E的坐标
（２）ΔAEC的面积
26.（6分）已知函数
与
的图象相交于点P，点P的纵坐标为4，求k的值。
27.（6分）请画出直线
向上平移5个单位后的图形，并求出该直线与两坐标轴所围成的三角形面积。
28. （6分） 正方形ABCD的边长为4，将此正方形置于平面直角坐标系中，使AB边落在X轴的正半轴上，且A点的坐标是（1，0）。
⑴求点B 、点C、点D的坐标；
⑵已知直线y = x - 经过点C，且与x轴交于点E，求四边形AECD的面积
 |
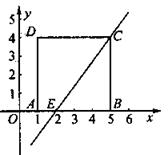29. (10分) 如图，表示一骑自行车和一骑摩托车者沿相同的路线由甲地到乙地行驶过程的函数图象，两地相距80千米，请根据图象解决下列问题：
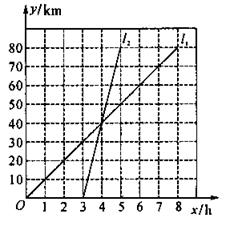⑴ l1是
行驶过程的函数图象，l2是
行驶过程的函数图象；
⑵ 哪一个人出发早？早多长时间？哪一个人早到达目的地？早多长时间？
⑶ 求出两个人在途中行驶的速度是多少？
⑷ 分别求出表示自行车和摩托车行驶过程的函数解析式，并求出自变量x的取值范围。