反比例函数练习卷
一、基础知识
1、一般地,形如 的函数称为反比例函数,比例系数为 。其中,自变量x的取值范围是 。
2、反比例函数的图象名称是 ,它有 个分支,并且随着x的不断增大(或减小),曲线越来越接近坐标轴。但永远不会与坐标轴相交。
3、反比例函数图象的性质:
| 表达式 | y=(k≠0) | |
| 图 象 | k>0 | k<0 |
|
|
| |
| 性 质 | 1.图象在第 、 象限; 2.在每个象限内,函数y的值随x的增大而 . | 1.图象在第 、 象限; 2.在每个象限内,函数y值随x的增大 . |
二、基础练习
(一)填空题
1、反比例函数![]() 的图象经过点P(-4,3),则k的值是
。
的图象经过点P(-4,3),则k的值是
。
2、若一反比例函数的图象经过点(1,2)则函数的解析式是 。
3、某厂有煤1500吨,求得这些煤能用的天数y与平均每天用煤吨数x之间的函数关系式为 。
4、下列函数:①xy=![]() ;②y=5-x;③
;②y=5-x;③![]() ;④
;④![]() ;⑤y=-3x;其中是反比例函数的是 。
;⑤y=-3x;其中是反比例函数的是 。
5、若反比例函数![]() 在每个象限内y随x的增大而增大,则k= 。
在每个象限内y随x的增大而增大,则k= 。
6、若函数![]() 为反比例函数,则m=
。
为反比例函数,则m=
。
7、若点(-2,-1)在反比例函数![]() 的图象上,则当x>0时,y随x的增大而
。
的图象上,则当x>0时,y随x的增大而
。
8、反比例函数![]() 的图象经过P(3,7)和Q(1,m)两点,则k= ,m=
。
的图象经过P(3,7)和Q(1,m)两点,则k= ,m=
。
9、反比例函数![]() 图象的两个分支分别位于
。
图象的两个分支分别位于
。
10、若反比例函数![]() 的图象位于一、三象限内,正比例函数
的图象位于一、三象限内,正比例函数![]() 过二、四象限,则k的整数值是 。
过二、四象限,则k的整数值是 。
11、点P既在反比例函数![]() (k≠0)的图象上,又在正比例函数y=-x的图象上,则点P的坐标是
。
(k≠0)的图象上,又在正比例函数y=-x的图象上,则点P的坐标是
。
 12、正比例函数y=mx与反比例函数
12、正比例函数y=mx与反比例函数![]() 的一个交点A的坐标为(3,2),则它们的另一个交点坐标为
。
的一个交点A的坐标为(3,2),则它们的另一个交点坐标为
。
13、如果一次函数y=mx+n与反比例函数![]() 的图象相交于点(
的图象相交于点(![]() ,2),那么这两个函数解析式分别为
、
。
,2),那么这两个函数解析式分别为
、
。
14、设有反比例函数![]() ,(
,(![]() )、
)、![]() 为其图象上两点,若
为其图象上两点,若![]() ,则k的取值范围是
。
,则k的取值范围是
。
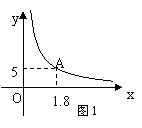
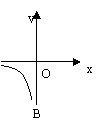
15、如图1,一定质量的氧气,其体积V(m3)是密度ρ(kg/m3)的反比例函数,其图象如图,这个反比例函数的解析式为 ,当ρ=1.5 kg/m3时的氧气的体积V= m3。
 16、y与k1x成反比例,z 与k2y成正比例,则z与x成 比例,比例系数为
。
16、y与k1x成反比例,z 与k2y成正比例,则z与x成 比例,比例系数为
。
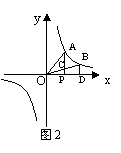
17、如图2,在x轴上,的点P的右侧有一点D,过点D作x轴的垂线交双曲线![]() 于点B,连结BO交AP于C,设△AOP的面积为S1,梯形BCPD面积为S2,则S1与S2的大小关系是S1
S2。(选填“>”“<”或“=”)
于点B,连结BO交AP于C,设△AOP的面积为S1,梯形BCPD面积为S2,则S1与S2的大小关系是S1
S2。(选填“>”“<”或“=”)
18、点P在反比例函数y=![]() 的图像上,若点P的纵坐标小于-1,则点P的横 坐标的取值范围是 。
的图像上,若点P的纵坐标小于-1,则点P的横 坐标的取值范围是 。
(二)选择题
 1、下列各点中,在函数
1、下列各点中,在函数![]() 的图象上的是( )
的图象上的是( )
A.(3,1) B.(-3,1) C.(![]() ,3) D.(3,
,3) D.(3,![]() )
)
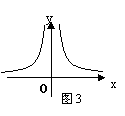
2、如图3所示的函数图象的解析式可能是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、函数![]() 的图象经点(1,-2),则函数y=kx+1的图象不经过( )
的图象经点(1,-2),则函数y=kx+1的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4、若点(3,4)是反比例函数![]() 图象上的一点,则此函数图象必经过点( )
图象上的一点,则此函数图象必经过点( )
A.(2,6) B.(2,-6) C.(4,-3) D.(3,-4)
5、已知点![]() 、
、![]() 、
、![]() 都在函数
都在函数![]() 的图象上,则下列关系式正确的是( )
的图象上,则下列关系式正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6、 在反比例函数y=
-![]() 的图象上有三点(x1,y1) ,(x2,y2)
,(x3,y3) , 若x1>x2>0>x3 ,则下列各式正确的是( )
的图象上有三点(x1,y1) ,(x2,y2)
,(x3,y3) , 若x1>x2>0>x3 ,则下列各式正确的是( )
A. y3 >y1 >y2 B. y3 >y2 >y1
C. y1 >y2 > y3 D. y1 >y3> y2
7、若M(![]() )、N
)、N![]() 、P
、P![]() 三点都在函数
三点都在函数![]() (k<0)的图象上,则
(k<0)的图象上,则![]() 的大小关系为( )
的大小关系为( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
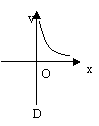
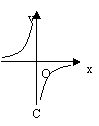
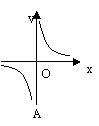
 8、已知一个矩形的面积为14cm2,其长为y cm,宽为x cm,则y与x之间的函数关系的图象大致是( )
8、已知一个矩形的面积为14cm2,其长为y cm,宽为x cm,则y与x之间的函数关系的图象大致是( )
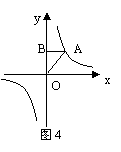
9、如图4,点A是![]() 图象上一点,AB⊥y轴于点B,则△AOB的面积是( )
图象上一点,AB⊥y轴于点B,则△AOB的面积是( )
A.1 B.2 C.3 D.4
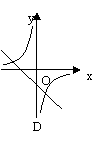
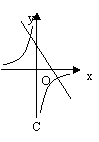
 10、反比例函数
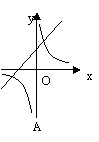
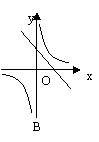
10、反比例函数![]() 和一次函数y=kx-k在同一直角坐标系中的图象 大致是( )
和一次函数y=kx-k在同一直角坐标系中的图象 大致是( )
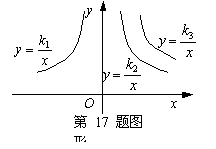 11、如图、如图是三个反比例函数
11、如图、如图是三个反比例函数![]() ,
,![]() ,
,![]()
在x轴上方的图象,由此观察得到![]() 、
、![]() 、
、![]() 的大
的大
小关系为( )
A、 ![]() B、
B、 ![]()
C、 ![]() D、
D、 ![]()
12、点A(a,b)、B(a-1,c)均在函数![]() 的图象上,若a<0,则b与c的大小关系是( )
的图象上,若a<0,则b与c的大小关系是( )
A.b>c B.b<c C.B=c D.b和c的大小关系不能确定
13、若函数y=k1x(k1≠0)和函数![]() 在同一坐标系内的图象没有公共点,则k1和k2( )
在同一坐标系内的图象没有公共点,则k1和k2( )
A.互为倒数 B.符号相同 C.绝对值相等 D.符号相反
14、已知反比例函数![]() 的图像经过P(m,n),则化简
的图像经过P(m,n),则化简![]() 的结果是( )
的结果是( )
A、2m2 B、2n2 C、n2-m2 D、m2-n2
15、一条直线与双曲线![]() 的交点是A(a,4),B(-1,b),则这条直线的解析式为( )
的交点是A(a,4),B(-1,b),则这条直线的解析式为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
三、综合应用
1、已知正比例函数y=kx与反比例函数![]() 的图象都过A(m,1)点,求此正比例函数解析式及另一个交点的坐标。
的图象都过A(m,1)点,求此正比例函数解析式及另一个交点的坐标。
2、一次函数y=ax+b和反比例函数![]() 的图象相交于M(2,2)、N(-4,-1)两点。
的图象相交于M(2,2)、N(-4,-1)两点。
求这两个函数解析式;
3、已知函数![]()
(1)m是何值时,它是反比例函数?
(2)它的图像位于哪些象限?y值怎样随x的变化而变化?
(3)当-4≤x≤-1时,函数值y的变化范围是什么?
4、已知y=y1+y2,y1是关于x+1的正比例函数,y2是关于x+1的反比例函数;当x=0时,y=-5,当x=2时,y=-7;(1)求y关于x的函数解析式;(2)当x=5时,求y的值。
5、已知函数![]() ,其中
,其中![]() 成正比例,
成正比例,![]() 成反比例,且当
成反比例,且当![]()
6、某汽车油箱的容积为80升,小陈把油箱注满油后从县城载客到400千米外的省城,把客人送到目的地后马上按原路返回,请回答下列问题:
(1)油箱注满后,汽车能够行驶的总路程a(单位:千米)与每千米平均耗油量b(单位:升)之间有怎样的函数关系?
(2)小陈以平均每千米耗油0.1升的速度驾驶汽车到达省城,在返回走了一半路程时下起了雨,小陈降低了速度,此时每行驶1千米的耗油量增加了一倍,如果小陈一直以此速度行驶,油箱里的油是否能回到县城?如果不够用,至少还需加多少油?
7、为了预防“非典”,学校对教室进行消毒,已知药物燃烧时,室内每立方米的含药量 y(毫克)与时间x(分钟)成正比例;药物燃烧后,y与x成反比例
(1) 分别求出药物燃烧时和药物燃烧后y与x的函数关系式
(2) 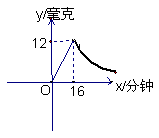 药物燃烧后,当空气中每立方米的含药量低于
药物燃烧后,当空气中每立方米的含药量低于![]() 时,学生方可进入教室,求经过多少分钟学生可进入教室?
时,学生方可进入教室,求经过多少分钟学生可进入教室?
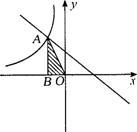 8、如图,Rt△AOB顶点A是一次函数
8、如图,Rt△AOB顶点A是一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的 图象在第二象限内的交点,且S△AOB=1,求A点坐标.
的 图象在第二象限内的交点,且S△AOB=1,求A点坐标.
 9、如图,正比例函数y=kx(k>0)与反比例函数
9、如图,正比例函数y=kx(k>0)与反比例函数![]() 的图象交于A、C两点,过A作x轴的垂线交x轴于B,连BC,求△ABC的面积。
的图象交于A、C两点,过A作x轴的垂线交x轴于B,连BC,求△ABC的面积。
10、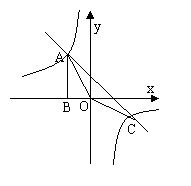 如图,Rt△ABO的顶点A是双曲线
如图,Rt△ABO的顶点A是双曲线![]() 与直线
与直线![]() 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥![]() 轴于B且S△ABO=
轴于B且S△ABO=![]()
(1)求这两个函数的解析式
(2)求直线与双曲线的两个交点
A,C的坐标和△AOC的面积。