育华学校2005年第一学期八年级期中测试
数学试卷（一）
一、相信自己都能选择对：在四个选项中只有一个正确的(10×3=30分)
1.若a>b,则下列不等式一定成立的是( )
A. 
B. 
C. –a>-b D.a-b>0
2.下列说法错误的是 （ ）
A.x<―3的整数解有无数个． B. x<５的整数解为x＝１，２，３，４
C. —
是－8x < 3的一个解． D. －6x < 2的解集是x>－
3.使代数式4x－
的值不大于3x+5的值的x的最大整数值是 （
）
A.不存在 B. 3 C. 6 D. 4
4． 下列说法中,正确的是 ( ).
A．中心对称图形必是轴对称图形.
B．矩形是中心对称图形,也是轴对称图形.
C．菱形是中心对称图形,但不是轴对称图形.
D．角是轴对称图形也是中心对称图形.
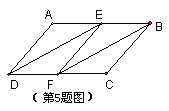5、如图所示，在□ABCD中，E、F分别AB、 CD的中点，连结DE、EF、BF，则图中平行四边形共有（ ）
A．2个 B．4个 C．6个 D．8个
6、平行四边形的周长为50，设它的长为x，宽
为y，则y与x的关系为（ ）
A、y=25－x B、y=25+x C、y=50－x D、y=50+x
7．下列语句中,不正确的是 ( ).
A．图形平移是由移动的方向和距离所决定;
B．图形旋转是由旋转中心和旋转角度所决定;
C．中心对称图形是旋转角度为180º的旋转对称图形;
D．旋转对称图形也是中心对称图形.
8、在平行四边形ABCD中，E、F分别为AB、AD的中点。G是CD上的点，且S□ABCD=1，则S△AEF和S△BEG分别等于（ ）
A. 
和
B.
和 C. 和
D. 和
9、平行四边形一边长是10㎝，那么这个平行四边形的两条对角线长可以是（ ）
A．4㎝和6㎝ B． 6㎝和8㎝ C． 20㎝和30㎝ D． 8㎝和12㎝
10、已知四边形ABCD中,AC交BD于点O,如果只给条件“AB∥CD”,那么还不能判定四边形ABCD为平行四边形,给出以下四种说法，其中正确的说法是 : （ ）
(1)如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;
(2)如果再加上条件“
”,那么四边形ABCD一定是平行四边形;
(3)如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形;
(4)如果再加上条件“AC=BD”,那么四边形ABCD一定是平行四边形
二、认真填写，相信你会轻松完成的：(10×3=30分)
11.已知关于x的不等式(2005-a)x>2005的解集是x<
,则a的取值
范围是
.
12、如图，绕着中心最小旋转 _ 度能与自身重合
13．如图所给的图形中只用平移可以得到的有（ ）个 ．
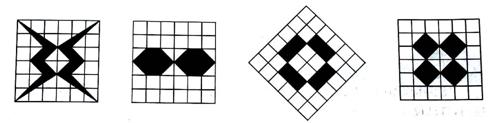
（第13题图）
14．在①平行四边形，②矩形，③菱形，④正方形中，一定能找到一点，使该点到各顶点的距离相等的图形有（ ）
15、用一根10㎝长的铁丝围成一个平行四边形使它的长边与短边的比为3:2，则它的四条边长分别为_______________________________。
16、如图16所示，图形①经过 _______ 变化成图形 ②,图形 ② 经过 ___
|
17、“x的
与8的差不大于0”用不等式表示为
。
18、如图，四边形ABCD是正方形，△CDE是等边三角形，
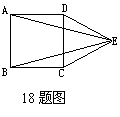那么∠AED=_________度.∠AEB=
.
19、要使一个□ABCD变成为菱形，需要增加一个条件： 。
20、已知，矩形ABCD的对角线AC、BD相交于点O，∠AOB=60º，AB=4㎝，则△AOB的形状是 三角形，AC长是 ㎝，BD长是
㎝.
三、解一解，并将解集在数轴上表示出来（2×5=10分）
21、1－
≥ x－
22、 3(x+3)<5(x-1)+7
四．做一做，相信你会有收获：
23.画出将左图绕O点逆时针转
的图形；然后将右图向右平移5格,再向下平移3格，画出经过两次平移后得到的图形（6分）
24、工人师傅做铝合金窗框分下面三个步骤进行:（8分）
(1)先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
(2)摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是: 。
(3)将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是: 。
|
25、如图B-1，平行四边形ABCD中，EF与AC相交于O，与边AD、BC分别相交于点E、F，且BF=DE. （8分）
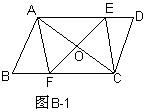（1）试说明四边形AECF是平行四边形。
（2）当EF与AC有怎样的关系时，四边形AECF是菱形。
（3）当EF与AC有怎样的关系时，四边形AECF是矩形。
（4）当EF与AC有怎样的关系时, 四边形AECF是正方
形 .
26、如图,在△ABC中,D为BC边上的一动点(D点不与B、C两点重合)。DE//AC交AB于E点，DF//AB交AC于F点。（8分）
（1）试探索AD满足什么条件是，四边形AEDF为菱形，试着说说
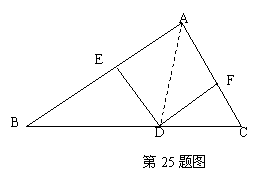你的理由；
（2）在（1）的条件下，△ABC满足什么条件时，四边形AEDF
为正方形，为什么？