2005年八年级(上) 数学第一次能力调查
一、选择题：（每题3分，共36分）
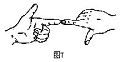
1、如图，两只手的食指和拇指在同一个平面内，
它们构成的一对角可看成是 （ ）
A、同位角 B、内错角 C、对顶角 D、同旁内角
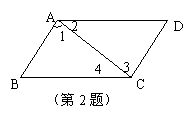
2、如图，若AB∥DC，那么 （ ）
A、∠1=∠3 B、∠2=∠4 C、∠B=∠D D、∠B=∠3
3、已知∠1和∠2是同旁内角，∠1=40°，∠2等于（ ）
A、160° B、140° C、40° D、无法确定
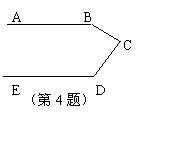
4、如图，已知AB∥ED，则∠B+∠C+∠D的度数是（ ）
A、180° B、270° C、360° D、450°
5、一架飞机向北飞行，两次改变方向后，前进的方向与原来的航行方向平行，已知第一次向左拐50°，那么第二次向右拐（ ）
A、40° B、50° C、130° D、150°
6、等边三角形的对称轴有 （ ）
A、1条 B、2条 C、3条 D、4条
7、等腰三角形的顶角的外角为70°，那么一个底角的度数为（ ）
A、35° B、55° C、65° D、110°
8、以下列各数为边长，不能组成直角三角形的是（ ）
A、3，4，5 B、4，5，6 C、5，12，13 D、6，8，10
9、如图，在Rt△ABC中，CD是斜边AB上的中线，
则图中与CD相等的线段有（ ）
A、AD与BD B、BD与BC
C、AD与BC D、AD、BD与BC
10、△ABC中，∠A：∠B：∠C=4：5：9，则△ABC是（ ）
A、直角三角形，且∠A=90° B、直角三角形，且∠B=90°
C、直角三角形，且∠C=90° D、锐角三角形
11、若△ABC三边长a,b,c满足 a+b－7 +
a－b－1 +（c－5）2=0，则△ABC是（
）
A、等腰三角形 B、等边三角形
C、直角三角形 D、等腰直角三角形
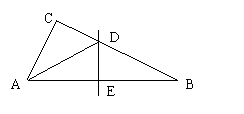12、如图，△ABC中，∠C=90°，AB的中垂线DE交AB于E，交BC于D，若AB=10，AC=6，则△ACD的
周长为（ ）
A、16 B、14 C、20 D、18
二、填空题：（每空格3分，共24分）
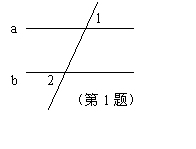
1、如图，若a∥b，∠1=40°，则∠2= 度；
2、如图，在长方形ABCD中，AB=3m，BC=2cm，则AB与CD之间的距离为 cm；
 | |||
 | |||
3、等边三角形的每个内角都等于 度；
4、已知一个等腰三角形的两边长分别是2和5，那么这个等腰三角形的周长为 ；
5、已知直角三角形的两直角边长为6cm和8cm，则斜边上的中线长是 cm，
斜边上的高为 cm；
6、如图，要为一段高为5米，长为13米的楼梯铺上红地毯，则红地毯至少要 米长；
 | |||
 | |||
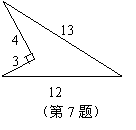
7、有一块田地的形状和尺寸如图所示，则它的面积为 。
三、解答题：（共7题，40分）
1、作图题：用刻度尺和圆规作一条线段，使它的长度为
cm。（5分）
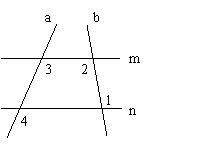
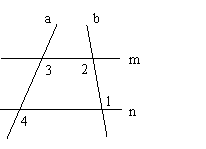
2、如图，∠1=100°，∠2=100°，∠3=120°，填空：（5分）
∵∠1=∠2=100°（已知）
∴ ∥ （
）
∴∠ =∠ （ ）
又∵∠3=120°（已知）
∴∠4= 度
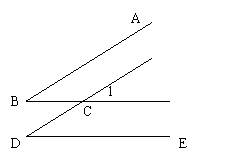
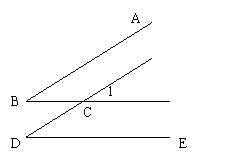3、如图，直线AB∥CD，DE∥BC，若∠B=（2x+15）°，∠D=(65－3x) °，
求∠1的度数。 （5分）
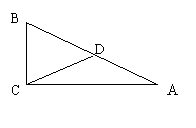
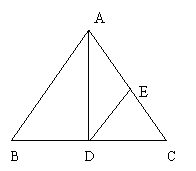
4、如图，AD是等腰三角形ABC的底边BC上的高，DE∥AB，交AC于点E，判断△ADE是不是等腰三角形，并说明理由。（5分）
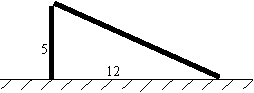
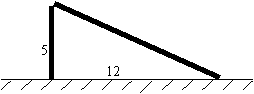
5、如图，一根竹竿在离地面5米处断裂，竹竿顶部落在离竹竿底部12米处，问竹竿折断之前有多长？（6分）
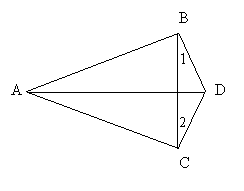
6、如图，∠ABD=∠ACD=90°，∠1=∠2，则AD平分∠BAC，请说明理由。（6分）
 |
7、如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD，
（1）求证：△BCE≌△DCF （4分）
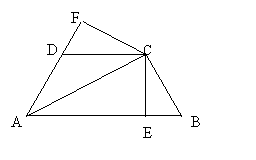（2）若AB=21，AD=9，BC=CD=10，求AC的长。 （4分）
2005年度第一学期八年级第一次月考数学答案
一、选择题（本题有12小题，每题3分，共36分，每小题只有一个选项是正确的，不选、多选、错选均不给分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | D | C | B | C | A | B | A | C | C | B |
二、填空题：（每空格3分，共24分）
1、 40 度 2、 2 cm 3、 60 度 4、 12
5、 5 cm, 4.8 cm 6、 17 米 7、 24
三、解答题：（共7题，40分）
1、作图题：（5分）
如图线段AB就是所求的线段
（作图正确得4分，结论1分）
 |
2、（5分）∵∠1=∠2=100°（已知）
∴ m ∥ n （内错角相等，两直线平行）
∴∠ 3 =∠ 4 （两直线平行，同位角相等）
又∵∠3=120°（已知）
∴∠4= 120 度
 |
3、（5分） 解：∵AB∥CD，DE∥BC
∴∠1=∠B，∠1=∠D
∴∠B=∠D
∴2x+15=65－3x （2分）
∴x=10
∴∠1=∠B=2x+15=35 （4分）
答：∠1的度数为35°。 （5分）
 |
4、（5分） 解：△ADE是等腰三角形，理由如下：
∵AD是等腰三角形ABC的底边BC上的高，
∴∠BAD=∠CAD（等腰三角形三线合一定理）
∵DE∥AB
∴∠BAD=∠ADE（两直线平行，内错角相等）
∴∠CAD=∠ADE
∴△ADE是等腰三角形
5、（6分）
解：∵52+122=169，
=13
（3分）
13+5=18 （5分）
∴竹竿折断之前的长度为18米。
6、（6分）
解：∵∠1=∠2 （已知）
∴BD=CD（一个三角形中，等边对等角）
∵∠ABD=∠ACD=90°（已知）
∴点D在∠BAC的角平分线上
∴AD平分∠BAC
7、
解：（1）（4分）∵AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，
∴∠CFD=90°，∠CEB=90°（垂线的意义）
CE=CF （角平分线的性质）
∵BC=CD （已知）
∴Rt△BCE≌Rt△DCF （HL）
（2）（4分） 由（1）得，
Rt△BCE≌Rt△DCF
∴DF=EB 设DF=EB=X
∵∠CFD=90°，∠CEB=90°，
CE=CF，AC=AC
∴Rt△AFC≌Rt△AEC （HL）
∴AF=AE
即：AD+DF=AB－BE
∵AB=21，AD=9，DF=EB=X
∴9+X=21－X 解得，X=6
在Rt△DCF中，∵DF=6，CD=10
∴CF=8
∴Rt△AFC中，AC2=CF2+AF2=82+（9+6）2=289
∴AC=17
答：AC的长为17。