2005—2006学年度第一学期八年级数学期末检测试题
一、选择题
1、下列四个实数中是无理数的是 ( ).
A.2.5
B.
C.π
D.1.414
2、下列计算正确的是
A·＝ B ＋＝ C ＝3 D ÷＝2
3、已知一组数据5，15，75，45，25，75，45，35，45，35，那么40时这一组数据的（ ）
A．平均数但不是中位数 B.平均数也是中位数
C．众数 D. 中位数但不是平均数
4、某人到瓷砖商店去购买一种多边形形状的瓷砖，用来铺设无缝地板，他购买的瓷砖形状不可以是（ ）
A.正三角形 B.矩形 C.正八边形 D.正六边形
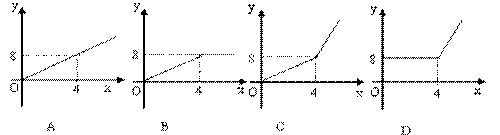
5、2004年6月3日中央新闻报道,为鼓励居民节约用水,北京市将出台新的居民用水收费标准:①若每月每户居民用水不超过4立方米,则按每立方米2元计算;②若每月每户居民用水超过4立方米,则超过部分按每立方米4.5元计算(不超过部分仍按每立方米2元计算).现假设该市某户居民某月用水
立方米,水费为
元,则与的函数关系用图象表示正确的是（ ）
 |
6、矩形ABCD中的顶点A、B、C、D按顺时针方向排列,若在平面直角坐标系内, B、D 两点对应的坐标分别是（2, 0）, (0, 0),且 A、C两点关于x轴对称.则C 点对应的坐标是
A（1, 1） B （1, －1） C （1, －2） D （, －）
7、将某个图形各点的横坐标变为原来的2倍，纵坐标变为原来的一半，则该图形（ ）
A、横向压缩为原来的一半，纵向伸长为原来的2倍
B、横向压缩为原来的一半，纵向压缩为原来的一半
C、横向伸长为原来的2倍，纵向压缩为原来的一半
D、横向伸长原来的2倍，纵向伸长为原来的2倍
8、长度为9、12、15、36、39的五根木棍，从中取三根依次搭成三角形，最多可搭成直角三角形的个数是（ ）
A．1 B．2 C．3 D．4
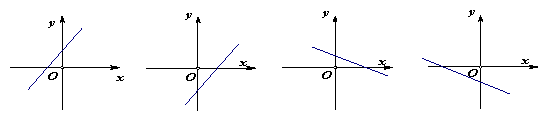7、已知正比例函数
（
）的函数值随的增大而增大，则一次函数
的图象大致是
（ ）
A B C D
10、下列美丽的图案，既是轴对称图形又是中心对称图形的个数是（ ）
 |
A、1个 B、2个 C、3个 D、4个
二：填空题(每小题题2分，共16分)
11、4的平方根是 ，－8的立方根是 。
12、正n边形的内角和等于1080°，那么这个正n边形的边数n=_____.
13、点（1，2）关于原点的对称点的坐标为 .
14、若函数
的图象经过点（－1，2），则k的值是 。
15、如图，□ABCD中，AE、CF分别是∠BAD和∠BCD的角平分线，根据现有的图形，请添加一个条件，使四边形AECF为菱形，则添加的一个条件可以是
（只需写出一个即可，图中不能再添加别的“点”和“线”）.
16、已知：在等腰梯形ABCD中，AD∥BC，对角线
AC⊥BD,AD=3cm,BC=7cm,则梯形的高是_______cm.
17、若三点A（0，3）、B（-3，0）、C（6，y）共线,则y=___________
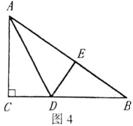
18、如图4，∠C=90°，AD平分∠BAC，DE⊥AB于E，
则BC=DB+CD=DB+________；若CD=3，AD=5，则AE=_______。
三、计算（每小题4分，共8分）
19. 化简下列各题：
(1)
20、解方程组（每小题5分，共10分）
 |
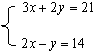① ②
|
1、请你作出四边形ABCD绕点O顺时针旋转90度后的图形。（6分）
 |
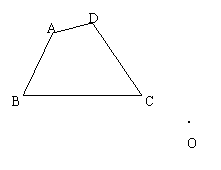2、，在方格直中建立直角坐标系，画出一次函数
y=4－2x的图像
五解答题
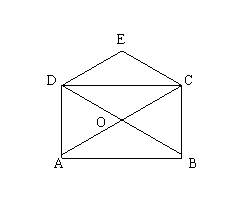
1、矩形ABCD的对角线相交于点O，DE//AC，CE//DB，CE、DE交于点E，请问：
四边形DOCE是什么四边形？请说明理由。
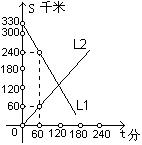2、（10分）A、B两辆汽车同时从相距330千米的甲、乙两地相向而行，s（千米）表示汽车与甲地的距离，t（分）表示汽车行驶的时间，如图，L1，L2分别表示两辆汽车的s与t的关系。
（1） L1表示哪辆汽车到甲地的距离与行驶时间的关系？
（2） 汽车B的速度是多少？
（3）求L1，L2分别表示的两辆汽车的s与t的关系式。
3、A、B两地相距36千米，甲乙两人同时从A、B两地出发相向而行，4小时相遇；若走6小时，甲所余路程是乙所余路程的两倍，求甲、乙速度。
4、阅读下列解题过程：
；
。
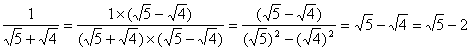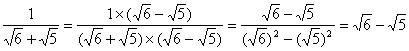请回答下列问题：
（1）观察上面的解题过程，请直接写出式子
；（5分）
（2）利用上面所提供的解法，请化简
的值。（5分）