| 县（区） 学校 姓名 座号 |
| …………………………………………………..密……………………………………….封……………………………………………….线…………………………………………………. |
双柏县2005年秋季学期教学质量监控检测
八年级数学试卷
（全卷满分100分，考试时间120分钟）
| 题 号 | 一 | 二 | 三 | 总 分 |
| 得 分 |
| 得 分 | 评卷人 |
一、填空题（每小题2分，共20分）
1、因式分解：ax－ay= 。
2、当x
时，分式
有意义。
3、已知x2－3x+k有一个因式（x－5），则k= 。
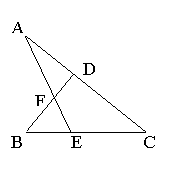4、如图，∠A
= 32°, ∠B = 45°，∠C
= 38°，
则∠DFE的度数为___________。
5、已知
则
。
6、等腰三角形的一条边的长是5，另一边长
是10，则它的周长是______ 。
7、如果x2－kx＋16是完全平方式，那么k= 。
8、化简：
=
。
9、在Rt△ABC中,∠ACB=90°,∠A=30°,且BC=4cm,则AC= cm。
10、已知等腰三角形的一个底角为80°,那么顶角的度数是 。
| 得 分 | 评卷人 |
二、选择题（每题只有一个正确的选项，小题3分，共30分）
11、下列各式中，正确的是（ ）
Ａ、
Ｂ、
Ｃ、
Ｄ、
12、在分式
中，最简分式有（ ）
Ａ、１个 Ｂ、２个 Ｃ、３个 Ｄ、４个
13、定理“三角形两边之和大于第三边”是根据以下哪个性质证明的（ ）
A、两点确定一条直线 B、垂线段最短
C、三角形的稳定性 D、两点之间线段最短
14、下列判断中，错误的是（ ）
A、若∠A+∠B=∠C，则△ABC为Rt△
B、若∠A=36°且∠B=2∠C，则△ABC为锐角三角形
C、若∠A与相邻的外角是89°，则△ABC为纯角三角形
D、若∠A∶∠B∶∠C=1∶2∶1，则△ABC为等腰直角三角形
15、给出下列命题：① 有三个角对应相等的两个三角形全等；
② 有三条边对应相等的两个三角形相等；
③ 有两边和一角对应相等的两个三角形全等；
④ 有两角和一边对应相等的两个三角形全等。
其中正确命题的个数是（ ）
A、1个 B、2个 C、3个 D、4个
16、如果把分式
中的x和y都扩大3倍，那么分式的值（ ）
A、不变 B、扩大3倍
C、缩小3倍 D、不能确定
17、等腰三角形的对称轴是（ ）
A、过顶点的直线 B、底边上的高线
C、底边上的中线所在的直线 D、腰上的高线所在的直线
18、在梯形面积公式
中，已知s、a、h且h≠0，则b的值为（ ）
A、
B、
C、
D、
19、一个三角形的两边分别是4和9，而第三边的长为奇数，则第三边的长是（ ）
A、3或5或7
B、9或11或13
C、5或7或9 D、7或9或11
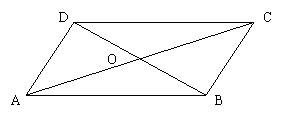
20、如图，AD∥BC，AD = BC，则图中所有
全等三角形对数为（ ）
A、2 B、3 C、4 D、5
| 得 分 | 评卷人 |
三、解答题（本大题满分50分）
21、（本小题6分）分解因式：
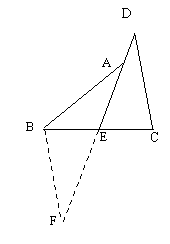
22、（本小题6分）在△ABC和△ADC中，给出下列三个论断：
①BC = DC； ②∠BAC =∠DAC； ③AB = AD。
请将其中两个论断作为条件，另一个论断作为结论构成一个真命题。然后写出证明过程。
 |
23、（本小题7分）化简求值： 
其中
24、（本小题6分）解方程：
25、（本小题7分）一组学生乘汽车去春游，预计共需车费120元，后来人数增了
，费用仍不变，这样每人少摊3元，原来这组学生的人数是多少？
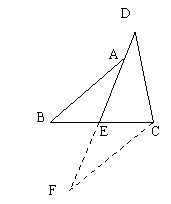
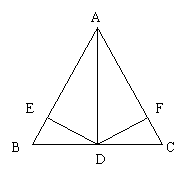26、（本小题8分）如图，△ABC中，AD是高线，DE⊥AB于E，DF⊥AC于F，且DE=DF . 求证：△ABC是等腰三角形.
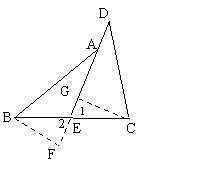
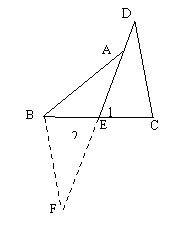
27、（本小题10分）阅读下面的题目及分析过程，并按要求进行证明。
已知：如图，E是BC的中点，点A在DE上，且∠BAE=∠CDE
求证：AB=CD
分析：证明两条线段相等，常用的一般方法是应用全等三角形或等腰三角形的判定和性质，观察本题中要证明的两条线段，它们不在同一个三角形中，且它们分别所在的两个三角形也不全等。因此，要证明AB=CD，必须添加适当的辅助线，构造全等三角形或等腰三角形。
现给出如下三种添加辅助线的方法，请任意选择其中两种 对原题进行证明。
（每种证明5分）
 |  | ||||
 | |||||
（1）延长DE到F （2）作CG⊥DE于G （3） 过C点作CF∥AB
使得EF=DE BF⊥DE于F交DE的延长线于F 交DE的延长线于F
双柏县2005年秋季学期教学质量监控检测八年级数学试卷参考答案
一、填空题（每小题2分，共20分）
1、a（x-y）； 2、≠－2； 3、－10； 4、115°； 5、3；
6、25；
7、±8；
8、x-2；
9、
；
10、20°
二、选择题（每题只有一个正确的选项，小题3分，共30分）
11、 B 12、B 13、D 14、B 15、B 16、A 17、C 18、A 19、D 20、C
三、解答题（本大题满分50分）
21、（本小题6分）分解因式： 22、（本小题6分）
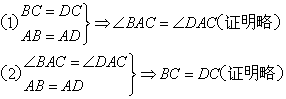
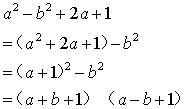
23、（本小题7分） 24、（本小题6分）
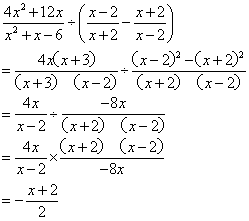
当 时，原式=
25、（本小题7分）解：设这组学生原有
人，依题意列方程：
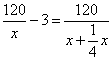即：
解得，x=8（经检验是原方程的根）
26、（本小题8分）
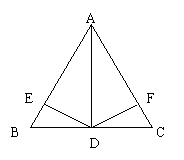证明： ∵DE⊥AB于E，DF⊥AC于F，
∴∠AED=∠AFD=90°
在Rt△AED和Rt△AFD中
DE=DF
AD=AD
∴Rt△AED≌Rt△AFD
∴∠1=∠2
∵AD是△ABC 的高
∴∠B=90°-∠1 ∠C=90°-∠2
∴∠B=∠C
∴AB=AC 即△ABC是等腰三角形
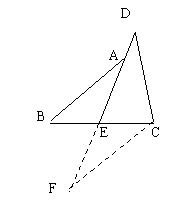27、（本小题10分）
 | |||
 | |||
（1）延长DE到F （2）作CG⊥DE于G （3） 过C点作CF∥AB
使得EF=DE BF⊥DE于F交DE的延长线于F 交DE的延长线于F
（1）证明：（注：选择以下其中的两种证明，每种给5分）
延长DE到F使得EF=DE，连接BF （2）作CG⊥DE于G，BF⊥DE于
在△DEC和△FEB中 F，交DE的延长线于F
DE=FE
∵CG⊥DE BF⊥DE
∠1=∠2 ∴∠CGE=∠BFE=90°
BE=CE 在△CGE和△BFE中
∴△DEC≌△FEB
∠CGE=∠BFE
∴∠D=∠F DC=FB ∠1=∠2
∵∠BAE=∠D BE=CE
∴∠BAE=∠F ∴△CGE≌△BFE
∴BA=BF ∴BF=CG
∴AB=CD 在△ABF和△DCG中
∠BAF=∠CDG
∠BFA=∠CGD=90°
BF=CG
∴△ABF≌△DCG
∴AB=CD
（3）过C点作CF∥AB交DE的延长线于F
∵CF∥AB
∴∠BAE=∠F ∠B=∠FCE
在△ABE和△FCE中
∠BAE=∠F
∠B=∠FCE
BE=CE
∴△ABE≌△FCE
∴AB=FC
∵∠BAE=∠D 而∠BAE=∠F
∴∠D =∠F
∴CF=CD
∴AB=CD