7.探索多边形的内角和与外角和
8.平面图形的密铺
班级:___________________________姓名:___________________________
作业导航
了解多边形的有关概念,掌握多边形的内角和及外角和的性质,并能利用性质进行计算,体会化归与转化的数学思想方法.了解平面图形的密铺概念,会简单的平面图形的密铺方法.
一、选择题
1.一个六边形最少可以分割为三角形的个数是( )
A.3 B.4 C.5 D.6
2.如果一个正多边形的一个内角是135°,则这个正多边形是( )
A.正五边形 B.正六边形
C.正八边形 D.正十边形
3.如果一个多边形的每个内角都相等,且内角和为1440°,则这个多边形的外角是( )
A.30° B.36° C.40° D.45°
4.四边形的四个内角可以都是( )
A.锐角 B.直角 C.钝角 D.不能确定
5.在下面给出的同一种平面图形中,不能进行密铺的是( )
A.三角形 B.四边形
C.正五边形 D.正六边形
二、填空题
6.若一个角的两边与另一个角的两边分别垂直,则这两个角大小关系是_______.
7.一个多边形的内角和等于它的外角和的4倍,那么这个多边形是______边形.
8.若多边形的每一个外角都是15°,则这个多边形的边数是_______.
9.假若将n(n≥3)边形切去一角,则切去后的多边形的内角和与n边形的内角和之间的关系为_______.
10.用形状、大小完全相同的_______平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称作平面图形的_______.
三、解答题
11.一个n边形的每一个内角都相等,它的一个外角与一个内角度数之比是1∶3,求这个n边形的边数.
12.已知一个多边形有两个内角为直角,其余各角的外角都等于45°,那么这个多边形的边数是多少?
13.用边长相同的正三角形和正方形两种平面图形是否能进行密铺?如果能,请画出草图,说明铺法;如果不能,请说明理由.
14.用边长相同的正八边形和正方形两种平面图形是否能进行密铺?如果能,请画出草图,说明铺法;如果不能,请说明理由.
15.我们常见到如图那样图案的地面,它们分别是全用正方形或全用正六边形形状的材料进行密铺.问:
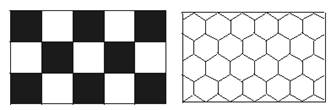
(1)能否全用正五边形的材料进行密铺,为什么?
(2)你能不能另外想出一个用一种多边形(不一定是正多边形)的材料进行密铺的方案,如果能,请把你想到的方案画成草图.
(3)请你再画出一个用两种不同的正多边形材料进行密铺的草图.
7.探索多边形的内角和与外角和 8.平面图形的密铺
一、1.B 2.C 3.B 4.B 5.C
二、6.相等或互补 7.十 8. 24 9.大180°或小180°或相等 10.一种或几种 镶嵌
三、11. 8 12. 6
13.能进行密铺(图略) 同一拼接点处有两个正方形和三个正三角形.
14.能进行密铺(图略) 同一拼接点处有两个正八边形和一个正方形.
15.(1)不能全用正五边形的材料进行密铺 (2)略 (3)略