4.矩 形 正方形
班级：___________________________姓名：___________________________
作业导航
理解并掌握矩形、正方形的性质及判别方法，会利用其性质和判别方法进行简单的推理和计算.
一、选择题
1.两条平行线被第三条直线所截，两组内错角的平分线相交所成的四边形是（ ）
A.一般平行四边形 B.菱形
C.矩形 D.正方形
2.四边形ABCD中，AC、BD相交于点O，能判别这个四边形是正方形的条件是（ ）
A.OA=OB=OC=OD，AC⊥BD
B.AB∥CD，AC=BD
C.AD∥BC，∠A=∠C
D.OA=OC，OB=OD，AB=BC
3.在矩形ABCD的边AB上有一点E，且CE=DE，若AB=2AD，则∠ADE等于（ ）
A.45° B.30° C.60° D.75°
4.矩形的一内角平分线把矩形的一条边分成3和5两部分，则该矩形的周长是（ ）
A.16 B.22 C.26 D.22或26
5.在正方形ABCD中，AB=12 cm，对角线AC、BD相交于O，则△ABO的周长是（ ）
A.12+12
B.12+6
C.12+ D.24+6
二、填空题
6.延长等腰△ABC的腰BA到D，CA到E，分别使AD=AB，AE=AC，则四边形BCDE是________，其判别根据是_______.
7.矩形的两条对角线的夹角是60°，一条对角线与矩形短边的和为15，那么矩形对角线的长为_______，短边长为_______.
8.矩形ABCD的周长是56 cm，它的两条对角线相交于O，△AOB的周长比△BOC的周长少4 cm，则AB=_______，BC=_______.
9.正方形的一条边长是3，那么它的对角线长是_______.
10.在一正方形的四角各截去全等的等腰直角三角形而得到一个小正方形，若小正方形的边长为1，那么所截的三角形的直角边长是________.
三、解答题
11.在四边形ABCD中，∠B=∠D=90°，且AB=CD，四边形ABCD是矩形吗？为什么？
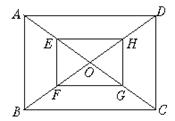
12.如图，矩形ABCD的对角线AC、BD相交于点O，E、F、G、H分别是OA、OB、OC、OD的中点，顺次连结E、F、G、H所得的四边形EFGH是矩形吗？说明理由.
13.E为正方形ABCD内一点，且△EBC是等边三角形，求∠EAD的度数.
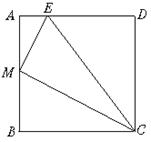
14.如图，正方形ABCD，AB=a，M为AB的中点，ED=3AE，（1）求ME的长；（2）△EMC是直角三角形吗？为什么？
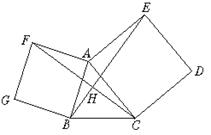
15.以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF，连结BE、CF，
（1）试探索BE和CF的关系？并说明理由.
（2）你能找到哪两个图形可以通过旋转而相互得到，并指出旋转中心和旋转角.
4.矩 形 正方形
一、1.C 2.A 3.A 4.D 5.A
二、6.矩形 对角线互相平分且相等的四边形是矩形 7. 10 5
8. 12 cm 16 cm 9. 3 10.
三、11.是矩形，连接AO，△ABC≌△CDA.
12.是矩形，OE=OF=OG=OH.
13. 15°
14.(1)
a (2)△EMC是直角三角形 理由略
15.（1）BE=CF，BE⊥CF
（2）△ABE和△AFC可以通过旋转而相互得到，旋转中心是A，旋转角为90°.