厦门市东山中学八年级（上）
数学期中考试卷
| 项目 | A卷 | B卷 | 总分 | |||
| 题号 | 一 | 二 | 三 | 四 | 五 | |
| 得分 | ||||||
一、耐心填一填！（每题3分）
1）一个正三角形绕着它的中心顺时针至少旋转 度能与原来的图形重合
2）请写出一个是中心对称但不是轴对称的图形
3）口ABCD的周长为60cm，对角线相交于点O，ΔAOB与ΔBOC的周长差为
8㎝，则四边形的边长为
4） 口ABCD中，∠A+∠C=220°， 则∠B=
5）在矩形ABCD中，对角线AC和BD相交于点O，∠AOB=120°，那么ΔBOC的形状是
6）菱形的周长是20㎝， 两个邻角的比是
，它的较短的对角线长是
7）梯形ABCD中，如果DC‖AB，AD=BC，∠A=60º，DB⊥AD，那么
∠DBC=
8）用不等式表示：a与b的差是非负数
9）已知绝对值
=3-5x，求x的取值范围是
10）在平行四边形中，一条对角线的长是10㎝，另一条对角线的长是12㎝，那么平行四边形的边长的取值范围是
二、精心选一选！（每题4分，共20分）
11、下列判定四边形是平行四边形的方法中，正确的个数有 （ ）
（1）一组对边平行， 另一组对边也平行
（2）一组对角相等， 另一组对角也相等
（3）一组对边平行， 另一组对边相等
（4）一组对边平行， 一组对角相等
A、1个； B、2个； C、3个 D、4个
12、平行四边形被一条对角线分得的两个三角形。 （ ）
A、 关于该对角线成轴对称 B、关于该对角线的中点成中心对称；
C、既关于该对角线成轴对称又关于该对角线的中点成中心对称；
D、既不关于该对角线成轴对称，又不关于该对角线的中点成中心对称；
13、在梯形ABCD中，AD‖BC，那么∠A：∠B：∠C：∠D可能是（ ）
A．1：2：3：4； B。1：2：4：3 ；C。4：3：2：1 ；D。1：4：2： 3
14、不等式
非负整数解的个数是
（ ）
A． 无数个；B。4个； C。3个.； D。0个
15、正方形具有而矩形不具有的性质是 （ ）
A、 内角和是360º； B、四个角都是直角；
C、两组对边分别相等 D、对角线平分对角
三、用心想与算！（总分50分）
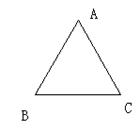
16、（本题6分）如图ΔABC是等边三角形，根据下列条件作图：
1. 画出ΔABC向北偏东30º方向平移AB长度后的图形；
2. 画出ΔABC向正东方向平移AB长度后的图形；
3. 画出当ΔABC绕顶点A逆时针方向旋转60º后的图形；
17、（本题14分。第1小题6分，第2小题8分）（1）x取何自然数时， 代数式
与
的差大于1？
2）解下列不等式，并把它解集在数轴上表示出来。
18、（本题10分）如图，在等腰梯形ABCD中，AB=DC，∠B=60º，DE ‖AB，试说明
（1） DE=DC
（2） △DEC是一个等边三角形。
19、（本题10分）把一堆苹果分给几个孩子， 如果每人分3个，那么多8个， 如果前面每人分5个，那么最后一人得到的苹果少于5个， 问几个孩子？有多少只苹果？
20、（本题10分）AOB是一条直线，OD为射线，OE平分∠AOD，OF平分∠DOB，DE⊥OE，DF⊥OF。（1）试说明OFDE是矩形。
（2）矩形OFDE被两条对角线分成四个小的三角形，如果四个小三角形的周长的和是86cm，对角线的长是13cm，那么矩形的周长是多少？
（B卷50分）
四、耐心填一填！(每题3分，共12分)
21、用不等号填空，如果a＞b，
那么ac2 bc2
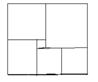22、如图是一块在电脑屏幕上出现的矩形色块图， 由6个颜色不同的正方形
组成， 设中间最小的正方形边长为1， 则这个矩形色块图
的面积为
23、把一张矩形ABCD的纸片，沿着EF折叠后，ED与BC交点为G，点D、
C分别落在D′、C′的位置上，如果∠EFG=55º，
那么∠EGB= 度
24、有以下命题正确的是
① 呈中心对称的两个图形的都是对应线段平行（或在同一条直线上）且相等，
对应点的连线被对称中心平分。
② 顺次连结矩形的各边中点的连线所组成的图形是正方形。
③ 如果（m-1）x<m-1的解集为X>1,那么m的取值范围是m>1.
④ 如a<b<c<d,那么
解集是b<x<c
以上正确命题是
五、用心去探究！（本题30分）
25、（本题8分）关于x、y 的方程组
的解满足0<x+2y<4,
求m的取值范围。
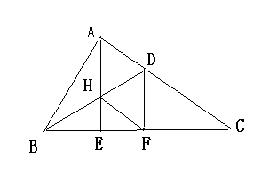
26、（本题10分）如图，△ABC中，∠BAC=90°，AE⊥BC于E，BD平分ABC，交AC于D，D F⊥BC于点 F ，AE交 BD于H，
1）试说明AHFD为菱形。
2）如果AB=FC，请你求出∠C的度数。
27、（本题10分）某景点的门票每张10元，一次性使用。考虑到人们的不同需求，也为了吸引更多的游客，该景点除了保留原来的售票方法外，还推出了一种“购买个人年票”的售票方法，（个人年票从购买日起，可供持票者使用一年），年票分为A、B、C三类：A类年票每张120元，持票进入景点时无需再购买门票；B类年票每张60元， 持票进入该景点时，需再购买门票， 每次2元；C类年票每张40元，持票进入该景点时，需再购买门票，每次3元。
1）如果你只选择一种购买门票的方式， 并且你计划在一年中用80元花在该景点的门票上，试通过计算，请你找出可进入该景点的次数最多的购买方式；
2）一年中进入该景点至少多少次时，购买A类年票比较合算。
28、（本题10分）在矩形ABCD中，AB=26㎝，AD=10㎝，动点P、Q分别从A、C两地出发，点P以每秒3㎝的速度向B移动，一直到点B止，点Q以每秒2㎝的速度向D移动。
（1）P、Q出发多少秒时，四边形PBCQ的面积为105㎝？
（2）是否存在某一时刻，使四边形PBCQ为正方形？如果存在，请求出该时刻，若不存在说明理由。
2004-2005学年八年级（上）
数学期中考试卷参考答案
一、填空题
1、120°
2、平行四边形（有多种情况）
3、11cm，9cm
4、70°
5、等边三角形
6、5cm
7、30°
8、
9、
10、
二、选择题
11、C12、B13、D14、B15、D
三、
16、
17、
18、
在数轴上表示为（略）
所以
（略）
19、
20、解设有x 个孩子
列式得：0〈3x+8-5（x-1）〈5
解得：4〈x〈6.5
符合条件的整数有5，6
答：如果有5个孩子，那么有23本书。如果有6个孩子，则有26本书。
20、用有三个角是直角的四边形是矩形证明。矩形的周长为34cm。
21、
22、143平方单位
23、110°
24、1：3：4
25、
、
（6分）
26、利用一组对边平行且相等判定ANFD为菱形。（过程略）（7分）
∠C=30°（3分）
27、（1）不可能买A类票；原来的购买方式为80/10=8次；B类为60+2x=80，最多可去10次，C类则为40+3x=80，最多可去13次，因此购买C类合算。（4分）
（2）设要进入x次，则有B 类为60+2x=120，最多可去30次，C类为40+3x=120，最多可去26次，用原有的方式购买最多去120/10=12次，因为10〈26〈30，因此至少进入30次时，购买A类合算。（6分）
28、设出发x秒后，面积为105平方cm，依据题意知PBCQ为直角梯形，所以面积为
（（26-3x）+2x）*10/2=105，
解得x=5
不可能为正方形，因为PB=10时，26-3x=10，运动时间为
秒，而CQ=10时，2x=10；
运动时间为5秒，时间不一致，因此不尊在这样的时刻。