一次函数
一. 填空
1.已知一个正比例函数的图象经过点（-2，4），则这个正比例函数的表达式是 。
2.若函数y= -2xm+2是正比例函数，则m的值是 。
1．若一次函数y=（2-m）x+m的图像经过第一、二、四象限，则m的取值范围是______．
2．在函数y=（m+6）x+（m-2）中，当_______时是一次函数．
3．已知点A（m，1）在直线y=2x-1上，则m=_________．
4．一次函数y=3x+m-1的图像不经过第二象限，则m的取值范围是________．
3.一次函数y= -2x+4的图象与x轴交点坐标是 ，与y轴交点坐标是 ，图象与坐标轴所围成的三角形面积是 。
8．若一次函数y=2x+b的图像与坐标轴围成的三角形的面积是9，则b=_______．
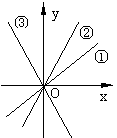4.如图：三个正比例函数的图像分别对应的解析式是①y＝ax，②y＝bx，③y＝cx，则a、b、c的大小关系是 ＞ ＞
。
5．已知一次函数y=-kx+5，如果点P1（x1，y1），P2（x2，y2）都在函数的图像上，且当x1<x2时，有y1<y2成立，那么系数k的取值范围是________．
4．当自变量x的值满足____________时，直线y=-x+2上的点在x轴下方．
5．已知直线y=x-2与y=-x+2相交于点（2，0），则不等式x-2≥-x+2的解集是________．
6．直线y=-3x-3与x轴的交点坐标是________，则不等式-3x+9>12的解集是________．6.已知一次函数y＝-x-(a-2)，当a_____时，函数的图象与y轴的交点在x轴的下方。
10.过点P(0，4)，且与直线y＝x－3平行的直线解析式为： ；将此直线沿y轴正方向平移2个单位后得到的直线解析式为： 。
6．已知直线y=kx+b和直线y=-3x平行，且过点（0，-2），则此直线与x轴的交点为________．
7.写出同时具备下列两个条件的一次函数表达式（写出一个即可） 。
（1）y随着x的增大而减小。 （2）图象经过点（1，-3）
8.某商店出售一种瓜子，其售价y（元）与瓜子质量x（千克）之间的关系如下表
| 质量x（千克） | 1 | 2 | 3 | 4 | …… |
| 售价y（元） | 3.60+0.20 | 7.20+0.20 | 10.80+0.20 | 14.40+0.2 | …… |
由上表得y与x之间的关系式是 。
9.某人用充值50元的IC卡从A地向B地打长途电话，按通话时间收费，3分钟内收费2.4元，以后每超过1分钟加收1元，若此人第一次通话t分钟（3≤t≤45），则IC卡上所余的费用y（元）与t（分）之间的关系式是 。
1．一次函数y=（m-2）x+（3-2m）的图像经过点（-1，-4），则m的值为（ ）．
A．-3 B．3 C．1 D．-1
2．函数y=-x-1的图像不经过（ ）象限．
A．第一 B．第二 C．第三 D．第四
3．若直线y=3x+6与坐标轴围成的三角形的面积为S，则S等于（ ）．
A．6 B．12 C．3 D．24
4．若一次函数y=（1-k）x+k中，k>1，则函数的图像不经过第（ ）象限．
A．一 B．二 C．三 D．四
5．一次函数y=kx+b满足x=0时y=-1；x=1时，y=1，则一次函数的表达式为（ ）．
A．y=2x+1 B．y=-2x+1
C．y=2x-1 D．y=-2x-1
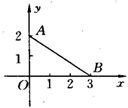
6．如图，线段AB对应的函数表达式为（ ）
A．y=-
x+2
B．y=-
x+2
C．y=-x+2（0≤x≤3） D．y=-x+20（0<x<3）
7．已知函数y=x-3，若当x=a时，y=5；当x=b时，y=3，a和b的大小关系是（ ）
A．a>b B．a=b C．a<b D．不能确定
8．若点P（a，b）在第二象限内，则直线y=ax+b不经过（ ）．
A．第一象限 B．第二象限 C．第三象限 D．第四象限
二．选择题（每题3分，共24分）
11.下列函数（1）y=πx
(2)y＝2x-1 (3)
(4)y＝2-1-3x
(5)y＝x2-1中，是一次函数的有（ ）
（A）4个 （B）3个 （C）2个 （D）1个
12.已知点（-4，y1），（2，y2）都在直线
上，则y1、 y2大小关系是( )
（A）y1＞y2 （B）y1＝y2 （C）y1＜y2 （D）不能比较
13.已知一次函数y＝kx＋b，当x增加3时，y减小2，则k的值是( )
(A) 
(B)
(C) 
(D)
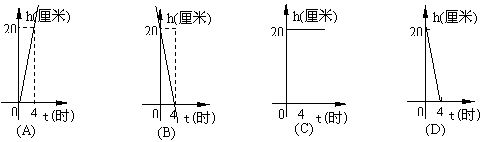
14.一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度n(厘米)与燃烧时间t(时)的函数关系的图象是( )
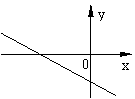15.已知一次函数y＝kx＋b的图象如图所示，则k、b的符号是( )
(A)k＞0，b＞0 (B)k＞0，b＜0
(C)k＜0，b＞0 (D)k＜0，b＜0
16.已知一次函数y＝ax＋4与y＝bx-2的图象在x轴上相交于同一点，则
的值是( )
(A) 4
(B) －2
(C) 
(D)
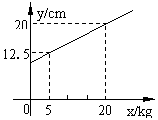
17.弹簧的长度y cm与所挂物体的质量x(kg)的关系是一次函数，图象如右图所示，则弹簧不挂物体时的长度是( )
(A)9cm (B)10cm (C)10.5cm (D)11cm
二. 解答题
19.(1)在同一坐标系中，作出函数y1＝-2x与
的图象；
(2)根据图象可知：方程组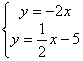
的解为
；
(3)当x 时，y2＜0。
2．（学科内综合题）已知一次函数y=（m-2）x+m2-6的图像与y轴相交，交点的纵坐标是-2，求m的值．
1.已知直线y=kx+b经过点A（0，－1）、B（2，1）、C（5，a），求
（1）此直线解析式 ，
（2）点C的坐标.
2.已知一次函数y=kx+b的图象经过点（－1，1）和点（1，－5），求当x=5时函数y的值.
3.一次函数y=kx+b的图象平行于正比例函数y=0.5x的图像，且过点（4，7），求一次函数的解析式以及与坐标轴的交点坐标.
4.已知一次函数y =kx+b在x =－4时,y =15,并且它的图象经过点( 6 , 5 ),求k、b的值
5.已知 y =kx+b的图象过点P(2 , 1),且与直线y =-2x-3没有交点,求这个一次函数解析式.
6.判断三点A（1，3）、B（ －2，0）、C（2，4）是否在同一条直线上
7.直线y=kx+b过点A（－1，5）且平行于直线y=－x.
（1）求这条直线的解析式；（2）若点B（m，－5）在这条直线上，求m及ΔAOB的面积.
8. 如果一次函数y =kx +b的自变量x的取值范围是－2≤x≤6,相应的函数值范围是－11≤y≤9,求此函数的解析式.
9.已知y－b 与x－a成正比例,当x =1时y = －2 ;当x = 3时y =2. 求y与x的解析式
10.直线L与直线y =2x+1的交点的横坐标为2，与直线y=－x+2的交点的纵坐标为1，求直线L的函数关系式.
2.一次函数的图象过A（2，4），B（0，2）两点，且与x轴交于点C. （1）求这个一次函数的解析式
（2）求ΔAOC的面积
20.已知一次函数y＝kx＋b的图象经过点(-1，-5)，且与正比例函数
的图象相交于点(2，a)，
求：(1)a的值。
(2)k、b的值。
(3)这两个函数图象与x轴所围成的三角形面积。
1．（学科内综合题）已知等腰三角形ABC的周长为10cm，底边BC的长为ycm，腰AB的长为xcm，试求y与x之间的函数关系式，并求x的取值范围．
21.一农民带上若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系，如图所示，结合图象回答下列问题。
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少?
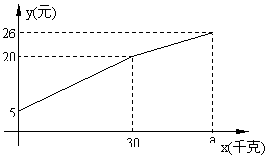(4)降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱(含备用零钱)是26元，试问他一共带了多少千克土豆？
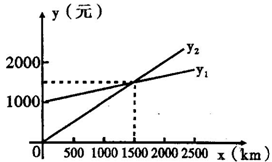
9．某单位需要用车，准备和一个体车主或一国有出租公司其中的一家签订合同，设汽车每月行驶xkm，应付给个体车主的月租费是y元，付给出租车公司的月租费是y元，y，y分别与x之间的函数关系图象是如图11-3-4所示的两条直线，观察图象，回答下列问题：
（1）每月行驶的路程在什么范围内时，租国有出租车公司的出租车合算？
（2）每月行驶的路程等于多少时，租两家车的费用相同？
（3）如果这个单位估计每月行驶的路程为2300km，那么这个单位租哪家的车合算？
