第十二章复习卷
一、 填空题：（每题3分，共30分）
1、□ABCD中，∠A+∠C=120°则∠D= 。
2、矩形两邻边之比为2：5，且周长为70㎝，则矩形的面积为 。
3、 以线段a=16，b=13为梯形两底，以c=10为一腰，则另一腰d的长度范围是 。
4、菱形的两条对角线长分别为4㎝，7㎝，则这个菱形的面积是 cm2。
5、在等腰梯形中一个角是60°，腰长是3 cm，则上下底的差为 cm。
6、矩形的两条对角线的夹角为60°，较短的边长为2 cm，则对角线长为 。
7、两条平行线被第三条直线所截，两组内错角的平分线相交所成的四边形是 。
8、菱形的周长是32cm，一个内角是30°，则菱形的面积是 cm2
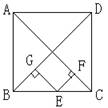9、如图，对角线为3㎝的正方形中，E为BC上一点，EF⊥AC于F，
EG⊥BD于G，那么EF+EG= 。
10、要做一个纸风筝，它的骨架为对角线互相垂直的等腰梯形，
若对角线长为1米，则需纸 平方米
二、 选择题：（每题3分，共24分）
1、下列条件不能确定平行四边形的是……………………………………………（ ）
A、AB∥CD，AD=BC B、AB=BC=CD=AD
C、OB=OD，OA=OC D、AB=CD，AB∥CD
2、一组对边平行，另一组对边相等的四边形是 ……………………………………（ ）
A、等腰梯形 B、平行四边形
C、矩形 D、等腰梯形或平行四边形
3、下列图形中是轴对称图形而不是中心对称图形的是……………………………（ ）
A、平行四边形 B、菱形 C、等腰梯形 D、直角梯形
4、正方形具有而菱形不一定具有的性质是……………………………………………（ ）
A、四边相等 B、对角线垂直且互相平分
C、对角线相等 D、对角线平分一组对角
5、用两个全等的直角三角形一定可拼成下列图形①平行四边形②矩形③菱形④正方形⑤等腰三角形⑥正三角形中的………………………………………………………（ ）
A、①④⑤ B、②⑤⑥
C、①②⑤ D、①②③
6、下面给出了四边形ABCD中∠A、∠B、∠C、∠D的度数之比，其中能说明四边形ABCD是平行四边形的是…………………………………………………………………（ ）
A、1：2：3：4 B、2：2：3：3
C、2：3：2：3 D、2：3：3：2
7、若菱形的周长是高的8倍，则菱形的较小内角的度数为…………………………（ ）
A、150° B、30° C、45° D、60°
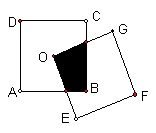8、如图，正方形ABCD的对角线相交于O，点O是正方形OEFG的一个顶点，如果两个正方形的边长都是4，则正方形OEFG绕点O无论怎样旋转，重叠部分面积都是……………………………（ ）
A、4 B、6 C、8 D、16
三、 解答题：（共46分）
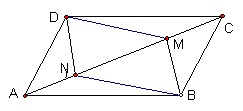1、如图，AC是平行四边形ABCD的一条对角线，AN=CM，试说明四边形BMDN是平行四边形。
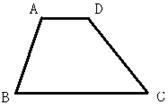
2、如图，在梯形ABCD中，AD∥BC，∠B=78°，∠C=51°，试说明AB=BC-AD
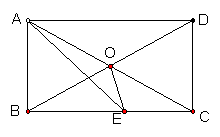3、如图，在矩形ABCD中对角线AC、BD交于点O，∠AOB=60°，AE平分∠BAD，交BC于点E，求∠BOE的度数。
4、若一个四边形各边依次是a、b、c、d，且满足a2+b2+c2+d2=2ac+2bd，试 判断四边形的形状并说明理由。
5、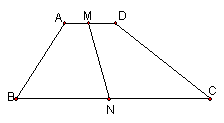
如图，梯形ABCD中，AD∥BC，∠B+∠C=90°，M、N分别是AD、BC的中点，试说明MN=1/2·（BC-AD）
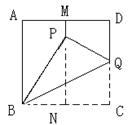6、如图，已知正方形纸片ABCD，M、N分别是AD、BC的中点，把BC边向上翻折，使点C恰好落在MN上的P处，BQ为折痕，求∠PBQ的度数。
四、提高题：（每题10分，共20分）
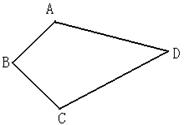
（1）如图，某村有一口呈四边形的池塘，在它的四个角处各有一棵桃树，现在村里准备开挖池塘建养鱼池，既想池塘面积扩大一倍，又想保持桃树不动，并要求扩建后的池塘成平行四边形，请问该村能否实现这一设想？若能，请你设计出并画出图形；若不能，请说明理由（保留作图痕迹，不写画法）。
 |
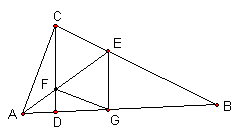（2）已知，如图，在△ABC中，∠ACB=90°，CD是高，AE是角平分线，交CD于点F，交BC于E，EG⊥AB，G是垂足，试说明：四边形CEGF是菱形。