初二数学期末复习卷
一、选择题（每小题3分，共30分）
1、在函数
中自变量x的取值范围是（ ）
A、x≥2 B、x≤2 C、x＞2 D、x＜2
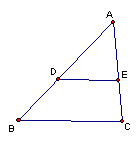
2、如图，已知DE∥BC，AD：DB=3：2，则DE：BC的值是（ ）
A、
B、
C、
D、
3、在△ABC中，∠C=90°，CosA=，那么Cot的值为（ ）
A、
B、
C、
D、
4、已知
，
，则
的值为（
）
A、3 B、4 C、5 D、6
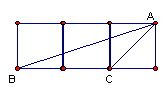
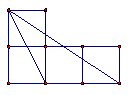
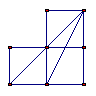
5、以下各图放置的小正方形的边长都相同，分别以小正方形的顶点为顶点画三角形，那么与△ABC相似的三角形的图形是（ ）
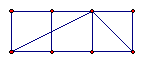
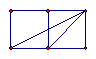
A B C D
6、下列各式中不正确的是（ ）
A、sin260°+cos260°=1 B、sin30°+cos30°=1
C、sin35°=cos55° D、tan45°＞sin45°
7、已知g=（m+1）
为反比例函数且图象位于第一、二象限，则m的值为（ ）
A、-3或1 B、3或-1 C、-3 D、1
8、如果直线y=kx+b与坐标轴两个交点分别为A（2，0）和B（0，-3），那么不等式kx+b+3≥0的解集是（ ）
A、x≥0 B、x≤0 C、x≥2 D、x≤-3
9、某次射击练习，甲、乙二人各射靶5次，命中的环数如下：
甲：7，8，6，8，6 乙：9，5，6，7，8
则射击技术较稳定的是
A.甲 B.乙 C.一样 D.不能确定
10、如图，AD∥BC，∠D=90°，DC=7，AD=2，BC=3. 若在边DC上有一点P,使
PAD与PBC相似,则这样的点P有（
）
A.1个 B.2个 C.3个 D.4个
二、填空题
11、在RT△ABC中，∠C=90°，cosA=，那么tanA=___________
12、若P（x，y）点到x轴的距离为3，到y轴的距离为5，则点P的坐标为________
13、已知x＜2，化简
=___________
14、如图，已知两点A（2，0），B（0，4）且∠1=∠2，那么点C的坐标为_________
15、如图,在RtABC中,CD是斜边AB上的高,
已知AD=32,BD=16,则tanA+tanB= .
16、设购买一张体育彩票中特等奖500万元的机会为a,抛掷一枚普通正方体骰子所得点数不小于3的机会为b,从一副扑克牌中随意抽取一张面值为4的机会为c.用“＜”将a、b、c进行排序为 .
17、已知一个样本标准差S=
,则样本的平均数为
,样本容量为
.
18、一个人坐在理发椅上理发，眼睛与前面墙上宽0.6米的镜子相距1米，他从镜子中恰好看到背后墙上宽2.4米的壁画，那么此镜面与背后墙壁的距离是______________
19、已知一次函数y=2x-b和反比例函数y=
的图象有两个交点，且其中一个交点的横坐标为3，那么另一个交点的坐标为___________
20、如图，矩形ABCD的一个内角平分线AE交BC与E，若AD=AE，那么tanα=__________
三、解答题
21、计算下列各式
（1）
（2）
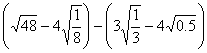
22、在RtABC中，∠C=90°，a=3，b=
.求∠A的四个三角函数值，并求∠A的度数.
23、（本题7分）如图，一水坝的横断面为梯形ABCD，坝顶DC宽5m，斜坡AD=6m，∠A=600，斜坡BC的坡度i=1：2．求坝底AB的长（精确到0.1m）．
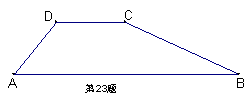
24、如图，边形DEFG是ΔABC的内接矩形，如果ΔABC的高线AH长8cm，底边BC长10cm，设DG=xcm，DE=ycm，求y关于x的函数关系式．
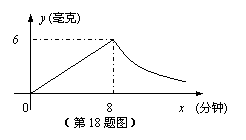
25、为了预防“非典”，某学校对教室采用药薰消毒。如图所示，已知药物燃烧是时，室内每立方米空气中的含药量y（毫克）与时间x（分钟）成正比例，药物燃烧完后，y与x成反比例。现测得药物8分钟燃烧毕，此时室内空气中每立方米的含药量为6毫克。请根据题中所提供的信息，解答下列问题：
（1）药物燃烧时y与x的函数关系式为 ，
自变量x的取值范围是： ；药物燃烧后y关于x的函数关系式为： 。
（2）研究表明，当空气中每立方米的含药量低于1.6毫克时学生方可进教室，
那么从消毒开始，至少需要经过 分钟后，学生才能回到教室；
（3）研究表明，当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？
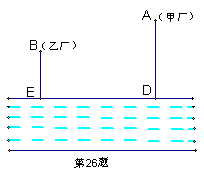26、如图，大江的一侧有甲、乙两家工厂，它们都有垂直于江边的小路AD、BE，长度分别为3千米和2千米，两条小路相距10千米．现在要在江边建一个抽水站，把水送到甲、乙两厂去．欲使供水管路最短，抽水站应建在哪里？