11.1.3 函数的图象
［要点再现］
1．一般地，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么在坐标平面内由这些点组成的图形，就是 。
2．描点法画函数图象的一般步骤是：(1) ；(2) ；
(3) 。
3．函数的表示方法共有 种。分别是 法、 法和
法。
4．你认为表示函数的几种方法各有什么优点？
［基础闯关］
1． 
下图是北京春季某一天的气温随时间变化的图象： 
根据图象回答，在这一天：
(1)8时、12时、20时的气温各是多少？
(2)最高气温与最低气温各是多少？
(3)什么时间气温最高，什么时间气温最低？
2． 请你仔细观察以下甲、乙两图，图中分别有几个变量？你能将其中的变量
看成另一个变量
的函数吗？为什么？
(甲) (乙)
3．如图：向放在水槽底部的烧杯注水（流量一定），注满烧杯后，继续注水，直至注满水槽，水槽中水面上升高度
与注水时间
之间的函数关系大致是下列图象中的（ ）
 | |||||
 | |||||
 | |||||
 | |||
 |
4．一种豆子每千克售2元，即单价是2元/千克。豆子的总的售价(元)与所售豆子的数量(千克)之间的函数关系可以表示成
。
(1)根据上面的函数解析式，给出一个值，就能算出的一个相应的值，这样请你完成下表：
|
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
|
|
(2)把与作为一对有序实数对，请你在坐标平面内描出上表中所得到的每一对有序实数(，)对相应的点。
(3)用线把上述的点连起来看看是什么图形？
［能力提升］
1.张爷爷晚饭以后外出散步，碰到老邻居，交谈了一会儿，返回途中在读报栏前看了一会儿报，下图是据此情景画出的图象，请你回答下面的问题：
(1)张爷爷在什么地方碰到老邻居的，交谈了多长时间？
(2)读报栏大约离家多少路程？
(3)张爷爷在哪一段路程走得最快？
(4)图中反映了哪些变量之间的关系？其中哪个是自变量？你能将其中某个变量看成另一个变量的函数吗？
2．一慢车和一快车沿相同路线从A地到相距120千米的B地，所行地路程与时间的函数图像如图所示.试根据图像，回答下列问题: ⑴慢车比快车早出发 小时，快车比慢车少用 小时到达B地；⑵快车用 小时追上慢车；
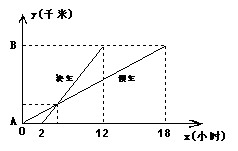此时相距A地
千米.
3．水管是圆柱形的物体，在施工中，常常如下图那样堆放，随着的增加，水管的总数是如何变化的？如果假设层数为
，物体总数为，
 | |||
 | |||
(1)请你观察图形填写下表，
|
| 1 | 2 | 3 | 4 | 5 | … |
|
| … |
(2)请你写出与的函数解析式并画出函数图象。
［考题追踪］
1．(2005年 陕西)甲、乙两同学从A地出发，骑自行车在同一条路上行驶到B地，他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系的图象如图所示，根据图中提供的信息，有下列说法：
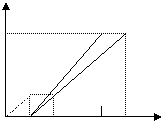(1). 他们都行驶了18千米；
s(千米) 乙 甲
(2). 甲在途中停留了0.5小时； 18
(3). 乙比甲晚出发0.5小时；
(4). 相遇后，甲的速度小于乙的速度；
(5). 甲乙两人同时到达目的地。
其中符合图象的描述的说法有：(
)
0 0.5 1 2 2.5 t(小时)
A. 2个 B. 3个 C. 4个 D.5个
2．如图中的图象（折线ABCDE）描述了一汽车在某一直线上的行驶过程中，汽车离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了120千米；②汽车在行驶途中停留了0.5小时；③汽车在整个行驶过程中的
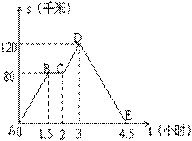平均速度为
千米/时；④汽车自出发后
3小时至4.5小时之间行驶的速度在逐渐减少.
其中正确的说法共有（ ）
A、1个 B、2个
C、3个 D、4个
11.1.3 函数的图象
［要点再现］
1． 函数图像 。
2． (1) 列表 ；(2) 描点 ；(3) 连线 。
3． 3 ， 关系式 、 图像 、 列表 。
4． 答：条形统计图能清楚的表示出每个项目的具体数据，
折线统计图能清楚的反映出事物的变化情况，
扇形统计图能清楚的表示出个部分在总体中所占的百分比。
［基础闯关］
1．答：(1)8时、12时、20时的气温各是8℃、10℃、10℃；
(2)最高气温与最低气温各是12℃、2℃；
(3)14时气温最高，4时气温最低 。
2．答：甲、乙两图，图中分别有2个变量：变量和变量；乙图中的变量看成另一个变量的函数：因为变量改变，变量也改变，并且对于每一个变量都有唯一的一个值与它对应；而甲图对于每一个变量有一个或两个值与它对应。
3． D
4． 
(1)
|
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
(2) 、(3)（图略）
［能力提升］
1. 答：(1)张爷爷在离家600米处碰到老邻居的，交谈了10分钟。
(2)读报栏大约离家300米
(3)张爷爷从读报栏回家这一段走得最快
(4)图中反映了距离与时间之间的关系。其中时间是自变量，能将路程看成时间的函数。
2．（1）2， 6 ；⑵ 2.5 ； 30 .
3． (1)
|
| 1 | 2 | 3 | 4 | 5 | … |
|
| 1 | 3 | 6 | 10 | 15 | … |
(2) 解：
（图略）
［考题追踪］
1． B 2 . B