初二数学阶段性测试卷
一、 填空题（3ˊ×10）
1、如图，已知∠1=70°，∠2=70°，∠3=100°，则∠4=
2、等腰三角形一个角的度数为50°，则顶角的度数为
3、当X
时，
有意义。
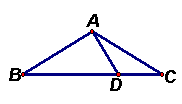
4、如图，△ABC中，AB=AC，∠C=30°，AB⊥AD，若AD=6cm，则BC=
5、△ABC中，AB=AC，∠B=40°，AD是BC边上的中线，则∠BAD=
6、如图，在平静的湖面上，有一支红莲，高出水面1米，一阵风吹来，红莲吹到一边，花朵齐及水面，已知红莲移动的水平距离为2米，则这里的水深是 米
（第1题） （第4题） （第6题）
7、如图，Rt△ABC中，CD是斜边AB上的高线，若AC=6，AB=10，则CD=
8、三角形的三边a,b,c满足
则△ABC的形状是
9、如图，△ABC是正三角形，D、E分别是AB、AC边上的点，且AE=BD ，CD、BE相交于点O，则∠EOC=
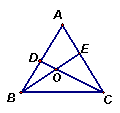
（第7题） （第9题）
10、某市自来水公司按如下标准收费：每户每月用水不超过5
，则每立方米收费1．5元；若每户每月用水超过5，则超过部分每立方米收费2元，小颖家每月的水费不少于20元，设她家每月的用水量是x，根据题意列
二、选择题（3ˊ×10）
1、下列图形中不是轴对称图形的是 （ ）
2、若a＜b，则下列各式不正确的是 （ ）
A．a-8＜b-8 B．
＜
C．-a＞-b
D．
＜
3、正三角形的边长为2，则它的面积是 （ ）
A．1
B．2
C．
D．
4、下列说法正确的是 （ ）
A．有一个锐角和一条边分别相等的两个直角三角形全等。
B．△ABC的三边a、b、c,若有
, 则△ABC是Rt△且∠C=90°
C．直角三角形斜边上的中线把这个直角三角形分成两个全等三角形
D．直角三角形斜边上的中线把这个直角三角形的面积平分
5、如图，用七巧板拼成的图形中，有多少个等腰直角三角形？ （ ）
A．7个 B．8个 C．9个 D．不确定
6、如图，△ABC中，∠C=Rt∠，AD平分∠BAC，BC=24，BD：CD=3：5，则点D到AB边的距离为 （ ）
A．3 B．9 C．12 D．15
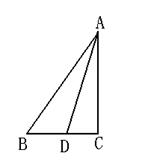
（第5题） （第6题） （第7题）
7、如图，在河上有两艘军舰A、B，则由A测得B的方向是 （ ）
A．南偏东30° B．北偏西30° C．南偏东60° D．北偏西60°
8、如图△ABC中，AB，AC边的中垂线相交于点O，且∠ABO=25°，∠BCO=30，则∠CAO的度数为 （ ） A．30° B．35° C．40° D．45°
9、如图，△ABC中，∠C=99°，AD交BC于D，把△ACD沿着直线BD翻折，使点D落在BC边上，如果恰有AD=BD，则∠B的度数是 （ ）
A．25° B．27° C．30° D．35°
10、如图、用不同颜色的马赛克覆盖一个圆形的台面，估计15°圆心角的扇形部分大约需要34片马赛克。已知每箱有125片马赛克片，那么应该购买多少箱马赛克片才能铺满整个台面 （ ）
A．5～6箱 B．6～7箱 C．7～8箱 D．8～9箱
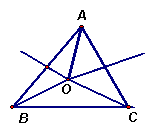
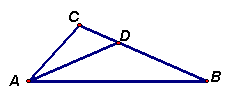
（第8题） （第9题） （第10题）
三、解答题（40ˊ）
1、如图，Rt△ABC中，∠C=Rt∠，∠A=40°，BE平分∠ABC，DE∥BC交AB于D，求∠DEB的度数。（5ˊ）
2、解不等式（组），（12ˊ）
（1） 解不等式 3X-5＜4X-3（X-1）并把解在数轴上表示出来
（2）
（3） 求不等式组：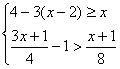
的非负整数解。
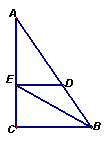
3、如图，四边形ABCD中，BD是它的对角线，AE⊥BD于E，CF⊥BD于F，且AB=CD，BF=DE，说明AB∥CD的理由。（6ˊ）
4、下图正方形网格中每个小正方形的边长都是1，每个小格的顶点叫做格点。
以格点为顶点分别按下列要求画三角形。（6ˊ）
（1）使三角形的三边长为3、
、
（2）画一个钝角三角形使它的面积为2。
5、有一家工厂向银行贷款8万元，购进一台机器生产某种零件。已知零件的生产成本为每只5元，销售价为8元，应缴税款是销售额的10﹪，银行年利率为10﹪，要求经过一年一次性还清贷款。这个家庭工厂这一年至少要生产、销售多少只零件？
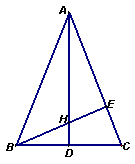
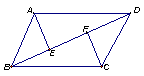
6、如图，△ABC中，AB=AC，AD⊥BC，BE⊥AC，且AE=BE。
（1）说明：△AEH≌△BEC的理由；
（2）猜想： AH与BD的长度是怎样的数量关系，并说明理由；
