2006—2007年度八年级上学期《一次函数》综合检测题
班级_______________ 姓名_____________ 座号______ 成绩__________
一、选择题（每小题3分，共30分）
1、对于圆的周长公式C=2πr，以下说法中正确的是（ ）
A、π是自变量 B、C是自变量 C、r是自变量 D、2πr是自变量
2、下列函数是一次函数，但不是正比例函数的为（ ）
A、
B、
C、
D、
3、若点A（2，4）在函数y=kx-2的图像上，则下列各点在此函数图像上的是（ ）
A、（0，-2） B、（
，0） C、（8，20） D、（
，）
4、函数
，自变量x的取值范围是（ ）
A、x≥-1 B、x
0 C、x>-1且
D、x≥-1且
5、一个矩形的周长为30，则矩形的面积y 与矩形一边长x的函数关系为（ ）
A、
B、
C、
D、
6、已知正比例函数y=（2m-1）x的图象上两点A（x1，y1），B（x2，y2），当x1 ＜x2时，有y1 ＞y2，则m的取值范围是（ ）
A、
B、
C、
D、
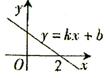7、函数y=kx+b（k、b为常数）的图象如图所示，则关于x的
不等式kx+b＞0的解集是（ ）
A、x＞0 B、x＜0
C、x＜2 D、x＞2
8、若函数y=-x+m与y=4x-1的图象交于x轴上一点，则m的值是( )
A、
B、 
C、
D、 
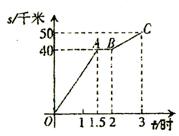9、小王于上午8时从甲地出发去相距50千米的乙地。图中折线OABC是表示小王离开甲地的时间t（时）与路程s（千米）之间的函数关系的
图象。根据图象给出的信息，下列判断中，错误的是（ ）
A、小王11时到达乙地
B、小王在途中停了半小时
C、与8：00—9：30相比，小王在10：00—11：00前进的速度比较慢
D、出发后1小时，小王走的路程少于25千米
10、若一次函数y=（3-k）x-k的图象经过第二、三、四象限，则k的取值范围是（ ）
A、k>3 B、0<k≤3 C、0≤k<3 D、0<k<3
二、填空题（每小题3分，共30分）
11、函数y=（m+6）x+（m-2），当m 时是正比例函数；当m 时它是一次函数。12、地壳的厚度约为8到40千米，在地壳以下不太深的地方，温度可按y=35x+t计算，
其中x（千米）是深度，t（℃）是地球表面温度，y（℃）是地表下x（千米）处的温
度，再这个关系式中， 和 是变量， 是 的函数，若地球
表面温度t=24℃，当x=20（千米）时,y= ℃。
13、把直线
向上平移3个单位所得到的直线的函数解析式为
。
14、二元一次方程2x+3y=5对应的一次函数（x为自变量）为 。
15、直线y=3x-4与坐标轴所围成的三角形的面积是 。
16、在同一直角坐标系中，两直线y=2x-1和y=2x+3的图象的位置关系为 ，d+3 由
此可知，方程组
的解的情况为
。
17、已知y-2与x成正比例，当x=3时，y=1，则y与x之间的函数关系式为 .。
18、某一次函数的图象经过点（-1，2），且函数y的值随自变量x的增大而减小，请你写出一个符合上述条件的函数关系式： 。
19、如图，直线l1、l2的交点坐标可以看作方程组 的解。
20、用火柴棒按如图所示的方式搭一行三角形，搭一个三角形需3根火柴棒，搭2个三角形需5根火柴棒，，搭3个三角形需7根火柴棒，照这样的规律搭下去，搭n个三角形需要s根火柴棒，那么s关于n的函数关系式是 （n为正整数）搭35个三角形需 根火柴棒。
 | |||
 | |||
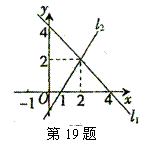三、解答题（共40分）
21、（4分）已知一次函数y=kx+b的图象经过三点A（2，0）、B（0，2）、C（m，3），求这个一次函数的解析式及m的值。
22、（7分）画出函数y=2x+6的图象，利用图象：（1）求方程2x+6=0的解；（2）求不等式2x+6＞0的解；（3）若-1≤y≤3，求x的取值范围。
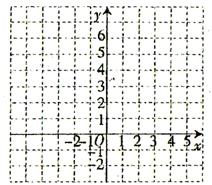
23（7分）某校厨房有一太阳能热水器，其水箱的最大蓄水量为1200升。已知水箱的蓄水量y（升）与匀速注水时间x（分钟），在没有放水的情况下有如下关系：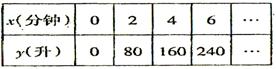
（1）根据上表中的数据，在图中的坐标系中描出相应的各点，顺次连接各点后，你发现这些点在哪一种图形上？猜一猜，符合这个图形的函数解析式；
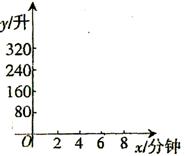（2）请验证上表各点的坐标是否满足函数解析式，归纳你的结论，并写出自变量x的取值范围。
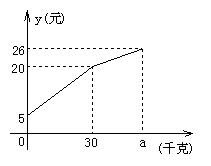
24.（10分）一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
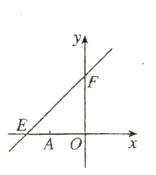
25、（12分）如图，直线y=kx+6与x轴y轴分别交于点E，F。点E的坐标为（-8，0），点A的坐标为（-6，0）。
（1）、求k的值；
（2）、若点P（x，y）是第二象限内的直线上的一个动点，当点P运动过程中，试写出
△OPA的面积S与x的函数关系式，并写出自变量x的取值范围；
（3）、探究：当P运动到什么位置时，△OPA的面积为
，并说明理由。