2006秋八年级课堂教学评估
数 学（第三章、图形的平移与旋转）
时限：90分钟 满分100分
姓名____________ 班级_____________ 成绩 ______________
一、填空题（每小题3分，共24分）
1．图形的平移、旋转、轴对称中，其相同的性质是_________．
2．经过平移，对应点所连的线段______________．
3．经过旋转，对应点到旋转中心的距离___________．
4．△ABC平移到△A′B′C′，那么S△ABC______S△A′B′C′．
5．等边三角形绕着它的三边中线的交点旋转至少______度，能够与本身重合．
6．甲图向上平移2个单位得到乙图，乙图向左平移2个单位得到丙图，丙图向下平移2个单位得到丁图，那么丁图向______平移______个单位可以得到甲图．
7．边长为4 cm的正方形ABCD绕它的顶点A旋转180°，顶点B所经过的路线长为______cm．
8．9点30分，时钟的时针和分针的夹角是______．
二、选择题（每小题3分，共30分）
1.下列图案中，可以由一个”基本图案”连续旋转
得到的是（
）.
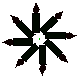
（A） （B） （C） （D）
2.图案（A）-（D）中能够通过平移图案（1）得到的是（ ）.
（1） （A） （B） （C） （D）
3.对图案的形成过程叙述正确的是（ ）.
（A）它可以看作是一只小狗绕图案的中心位置旋转90°、180°、270°形成的
（B）它可以看作是相邻两只小狗绕图案的中心位置旋转180°形成的
（C）它可以看作是相邻两只小狗绕图案的恰当的对称轴翻折而成的
（D）它可以看作是左侧、上面的小狗分别向右侧、下方平移得到的
4.下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的，每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的，旋转的角度为（ ）.
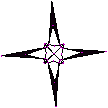
（A）
（B）
（C）
（D）
5. 如图1，ΔABC和ΔADE都是等腰直角三角形，∠C和∠ADE都是直角，点C在AE上，ΔABC绕着A点经过逆时针旋转后能够与ΔADE重合得到图1，再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图2.两次旋转的角度分别为（ ）.
（A）45°，90°（B）90°，45°（C）60°，30°（D）30°，60°
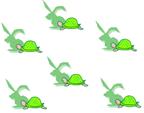
图1 图2
6.“龟兔赛跑”的故事图案的形成过程叙述不正确的是（ ）.
（A）它可以看作是一个龟兔图案作为”基本图案”经过平移得到的.
（B）它可以看作是上面三个龟兔图案作为”基本图案”经过平移得到的.
（C）它可以看作是相邻两个龟兔图案作为”基本图案”经过平移得到的.
（D）它可以看作是左侧两个龟兔图案作为”基本图案”经过平移得到的.
7.下列图案中，不可以由一个“基本图案”通过连续平移得到的是（ ）
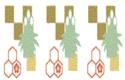
（A） （B） （C） （D）
8.下列图案都是在一个图案的基础上，在“几何画板”软件中拖动一点后形成的，它们的共性是都可以由一个“基本图案”通过连续旋转得来，旋转的角度是（ ）.
（A） （B） （C） （D）
9.同学们曾玩过万花筒，它是由三块等宽等长的玻璃片围成的.如图是看到的万花筒的一个图案，图中所有小三角形均是全等的等边三角形，其中的菱形AEFG可以看成是把菱形ABCD以A为中心（ ）.
（A）顺时针旋转60°得到（B）顺时针旋转120°得到
（C）逆时针旋转60°得到（D）逆时针旋转120°得到
10. 下列这些复杂的图案都是在一个图案的基础上，在“几何画板”软件中拖动一点后形成的，它们中每一个图案都可以由一个“基本图案”通过连续旋转得来，旋转的角度是（ ）
（A）
（B） （C） （D）
三、解答题（9、10小题每小题5分，11～21小题每小题6分，共76分）
1．(4分)请画一个圆，画出圆的直径AB，分析直径AB两侧的两个半圆可以怎样相互得到？
2．(4分)过等边三角形的中心O向三边作垂线，将这个三角形分成三部分．这三部分之间可以看作是怎样移动相互得到的？你知道它们之间有怎样的等量关系吗？
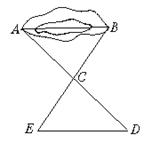
3．(5分)如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个可以直接到达A和B的点C，连结AC并延长到D，使CD=CA．连结BC并延长到E，使CE=CB．连结DE，那么量出DE的长，就是A、B的距离，为什么？线段DE可以看作哪条线段平移或旋转得到．
4．(5分)画线段AB，在线段AB外取一点O，作出线段AB绕点O旋转180°后所得的线A′B′．请指出AB和A′B′的关系，并说明你的理由．
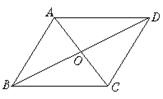
5．(6分)如图，四边形ABCD是平行四边形．
（1）图中哪些线段可以通过平移而得到；（2）图中哪些三角形可以通过旋转而得到．
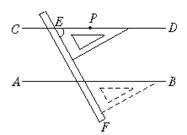
6．(4分)同学们用直尺和三角板画平行线，这种画平行线的方法利用了怎样的移动？由此我们得出了什么结论？
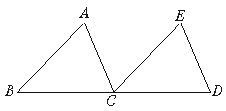
7．(4分)如图，△ABC通过平移得到△ECD，请指出图形中的等量关系．
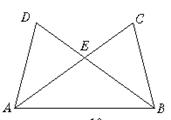
8．(4分)请你指出△BDA通过怎样的移动得到△CAE．
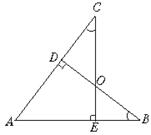
9．(4分)如图，你能说明△ABC通过怎样的移动可以得到△BAD吗？
10．(6分)由一个半圆（包含半圆所对的直径）和一个长方形组成一个“蘑菇”图形，将此图形作为“基本图形”经过两次平移后得到一组图案．这样的图案是否可作为公园中“凉亭”的标志呢？请你设计一下这个标志．
参考答案
一、1．图形的形状、大小不变，只改变图形的位置
2．平行且相等 3．相等 4．等于 5．120 6．右 2 7．4π 8．105°
二、1、 解：（B）.2、 解：（B） 3、 解：选（D） 4、解：（D） 5、解：（A） 6、 解；选（C）.7、 解：（C） 8、 解：（D）.9、解：选（D）10、解：（C）.
三、1．绕圆心旋转180°或以直线AB为对称轴翻折 2．旋转120°，它们是全等四边形，面积相等，对应线段、对应角相等
3．△ABC≌△DCE，AB=DE，线段DE可看作AB绕点O旋转180°得到
4．AB∥A′B′，且AB=A′B′，△AOB≌△A′OB′
5．(1)AB和DC，AD和BC （2）△AOB和△COD，△BOC和△DOA，△ABC和△CDA，△ABD和△CDB
6．平移，平行公理：同位角相等两直线平行
7．AB=EC，AC=ED，BC=CD，∠A=∠E，∠B=∠ECD，∠ACB=∠D，∠A=∠ACE
8．△BDA先绕点A逆时针旋转，使DA和AB在一条直线上，然后再以过A点垂直AB的直线为对称轴作它的对称图形．（或将△BDA绕点A顺时针旋转∠CAB，再以AE为对称轴翻折）
9．先将△ABC沿直线AB向左平移，使点B与点A重合，然后再以过A点且垂直于AB的直线为对称轴翻折．
10．略